इस लेख में हम यथासंभव पूरी तरह से ट्रेपोजॉइड के गुणों को प्रतिबिंबित करने का प्रयास करेंगे। विशेष रूप से, हम एक ट्रेपेज़ॉइड के सामान्य संकेतों और गुणों के बारे में बात करेंगे, साथ ही एक खुदा हुआ ट्रेपोज़ॉइड के गुणों के बारे में और एक ट्रेपोज़ॉइड में खुदे हुए सर्कल के बारे में बात करेंगे। हम एक समद्विबाहु और आयताकार समलंब के गुणों पर भी चर्चा करेंगे।

माना गुणों का उपयोग करके किसी समस्या को हल करने का एक उदाहरण आपको अपने सिर में स्थानों को सुलझाने और सामग्री को बेहतर ढंग से याद रखने में मदद करेगा।

ट्रेपेज़ॉइड और ऑल-ऑल-ऑल

शुरू करने के लिए, आइए संक्षेप में याद करें कि एक ट्रेपोजॉइड क्या है और इसके साथ अन्य अवधारणाएं क्या जुड़ी हैं।

तो, एक समलम्ब चतुर्भुज आकृति है, जिसकी दो भुजाएँ एक दूसरे के समानांतर हैं (ये आधार हैं)। और दो समानांतर नहीं हैं - ये पक्ष हैं।

ट्रेपेज़ॉइड में, ऊंचाई को कम किया जा सकता है - आधारों के लंबवत। मध्य रेखा और विकर्ण खींचे जाते हैं। समलम्ब चतुर्भुज के किसी भी कोने से एक द्विभाजक खींचना भी संभव है।

अब हम इन सभी तत्वों और उनके संयोजनों से जुड़े विभिन्न गुणों के बारे में बात करेंगे।

समलम्बाकार विकर्णों के गुण

इसे स्पष्ट करने के लिए, पढ़ते समय, कागज के एक टुकड़े पर एक AKME समलम्बाकार रेखाचित्र खींचिए और उसमें विकर्ण खींचिए।

1. यदि आप प्रत्येक विकर्ण के मध्यबिंदु पाते हैं (इन बिंदुओं को X और T से निरूपित करते हैं) और उन्हें जोड़ते हैं, तो आपको एक खंड मिलता है। समलम्ब चतुर्भुज विकर्णों के गुणों में से एक यह है कि XT खंड मध्य रेखा पर स्थित है। और इसकी लंबाई को आधार अंतर को दो से विभाजित करके प्राप्त किया जा सकता है: एक्सटी = (ए - बी) / 2.
2. हमसे पहले AKME का वही समलंब है। विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। आइए त्रिभुज AOE और MOC पर विचार करें, जो त्रिभुज के आधारों के साथ विकर्णों के खंडों द्वारा बनाए गए हैं। ये त्रिभुज समान हैं। समलम्ब चतुर्भुज के आधारों के अनुपात के माध्यम से k त्रिभुजों की समानता का गुणांक व्यक्त किया जाता है: के = एई / केएम।
   त्रिभुज AOE और MOC के क्षेत्रफलों का अनुपात गुणांक k 2 द्वारा वर्णित है।
3. सभी समान समलम्बाकार, समान विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। केवल इस बार हम उन त्रिभुजों पर विचार करेंगे जो समलंब के पार्श्व पक्षों के साथ मिलकर बने विकर्णों के खंड हैं। त्रिभुज AKO और EMO के क्षेत्रफल समान हैं - उनके क्षेत्रफल समान हैं।
4. समलम्ब चतुर्भुज की एक अन्य संपत्ति में विकर्णों का निर्माण शामिल है। इसलिए, यदि हम छोटे आधार की दिशा में AK और ME के ​​पार्श्व पक्षों को जारी रखते हैं, तो देर-सबेर वे किसी बिंदु पर प्रतिच्छेद करेंगे। इसके अलावा, ट्रेपेज़ॉइड के आधारों के मध्य बिंदुओं के माध्यम से, एक सीधी रेखा खींचें। यह आधारों को X और T पर प्रतिच्छेद करता है।
   यदि हम अब लाइन XT का विस्तार करते हैं, तो यह समलम्बाकार O के विकर्णों के प्रतिच्छेदन बिंदु को एक साथ जोड़ देगा, वह बिंदु जिस पर पार्श्व पक्षों के विस्तार और X और T के आधारों के मध्य बिंदु प्रतिच्छेद करते हैं।
5. विकर्णों के चौराहे के बिंदु के माध्यम से, एक खंड बनाएं जो समलम्बाकार के आधारों को जोड़ता है (टी सीएम के छोटे आधार पर स्थित है, एक्स - बड़े एई पर)। विकर्णों का प्रतिच्छेदन बिंदु इस खंड को निम्नलिखित अनुपात में विभाजित करता है: TO / OX = KM / AE.
6. और अब, विकर्णों के चौराहे के बिंदु के माध्यम से, समलम्बाकार (ए और बी) के आधारों के समानांतर एक खंड बनाएं। चौराहा इसे दो बराबर भागों में विभाजित करेगा। आप सूत्र का उपयोग करके किसी खंड की लंबाई ज्ञात कर सकते हैं 2ab / (ए + बी).

समलम्बाकार केंद्र रेखा गुण

इसके आधारों के समानांतर समलम्बाकार में मध्य रेखा खींचिए।

1. एक ट्रेपेज़ॉइड की मध्य रेखा की लंबाई की गणना आधारों की लंबाई को जोड़कर और उन्हें आधे में विभाजित करके की जा सकती है: एम = (ए + बी) / 2.
2. यदि आप समलम्ब चतुर्भुज के दोनों आधारों से कोई खंड (उदाहरण के लिए ऊँचाई) खींचते हैं, तो मध्य रेखा उसे दो बराबर भागों में विभाजित कर देगी।

समलम्ब चतुर्भुज का द्विभाजक गुण

समलम्ब चतुर्भुज के किसी भी कोने को चुनें और एक द्विभाजक बनाएं। उदाहरण के लिए, हमारे AKME समलम्बाकार का KAE कोण लें। निर्माण को स्वयं पूरा करने के बाद, आप आसानी से यह सुनिश्चित कर सकते हैं कि द्विभाजक आधार से कट जाता है (या आकृति के बाहर एक सीधी रेखा पर इसकी निरंतरता) पक्ष के समान लंबाई का एक खंड।

समलंब कोण गुण

1. आप पार्श्व भुजा से सटे कोनों के दो युग्मों में से जो भी चुनें, एक युग्म में कोणों का योग हमेशा 180 0: α + β = 180 0 और + = 180 0 होता है।
2. ट्रेपेज़ॉइड बेस के मध्य बिंदुओं को TX सेगमेंट से कनेक्ट करें। अब आइए समलम्ब चतुर्भुज के आधार पर कोनों को देखें। यदि उनमें से किसी पर कोणों का योग 90 0 है, तो TX खंड की लंबाई की गणना आसानी से आधारों की लंबाई में अंतर के आधार पर की जा सकती है, जिसे आधे में विभाजित किया गया है: TX = (एई - केएम) / 2.
3. यदि समलम्ब चतुर्भुज के कोने के किनारों के माध्यम से समानांतर सीधी रेखाएँ खींची जाती हैं, तो वे कोने की भुजाओं को आनुपातिक खंडों में विभाजित कर देंगी।

एक समद्विबाहु (समद्विबाहु) समलम्बाकार के गुण

1. एक समद्विबाहु समलम्ब में, किसी भी आधार पर कोण बराबर होते हैं।
2. अब ट्रेपोजॉइड को फिर से बनाएं ताकि यह कल्पना करना आसान हो जाए कि यह किस बारे में है। AE के आधार को बारीकी से देखें - M के विपरीत आधार का शीर्ष उस रेखा पर एक बिंदु पर प्रक्षेपित होता है जिसमें AE होता है। शीर्ष A से शीर्ष M के प्रक्षेपण बिंदु तक की दूरी और समद्विबाहु समलंब की मध्य रेखा समान हैं।
3. समद्विबाहु समलम्बाकार विकर्णों की संपत्ति के बारे में कुछ शब्द - उनकी लंबाई समान है। और इन विकर्णों के झुकाव के कोण भी समलम्बाकार के आधार पर समान हैं।
4. केवल एक समद्विबाहु समलम्ब के चारों ओर एक वृत्त का वर्णन किया जा सकता है, क्योंकि चतुर्भुज 180 0 के विपरीत कोणों का योग इसके लिए एक पूर्वापेक्षा है।
5. समद्विबाहु समलम्बाकार की संपत्ति पिछले पैराग्राफ से इस प्रकार है - यदि एक वृत्त को समलंब के पास वर्णित किया जा सकता है, तो यह समद्विबाहु है।
6. समद्विबाहु समलम्बाकार की विशेषताओं से समलम्ब चतुर्भुज की ऊँचाई का गुण इस प्रकार है: यदि इसके विकर्ण समकोण पर प्रतिच्छेद करते हैं, तो ऊँचाई की लंबाई आधारों के योग के आधे के बराबर होती है: एच = (ए + बी) / 2.
7. समलम्ब चतुर्भुज के आधार के मध्य बिंदुओं के माध्यम से फिर से TX का एक खंड बनाएं - एक समद्विबाहु समलम्ब में, यह आधारों के लंबवत है। और साथ ही TX समद्विबाहु समलम्बाकार की सममिति की धुरी है।
8. इस बार, बड़े आधार से नीचे (इसे a से निरूपित करें) समलम्ब चतुर्भुज के विपरीत शीर्ष से ऊँचाई। दो खंड होंगे। एक की लंबाई पाई जा सकती है यदि आधारों की लंबाई को मोड़कर आधा कर दिया जाए: (ए + बी) / 2... दूसरा तब प्राप्त होता है जब हम छोटे को बड़े आधार से घटाते हैं और परिणामी अंतर को दो से विभाजित करते हैं: (ए - बी) / 2.

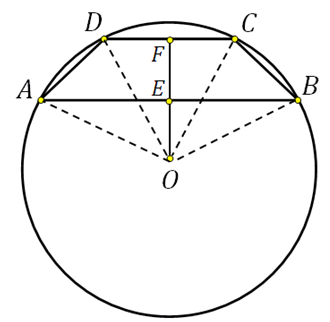
एक वृत्त में अंकित समलंब चतुर्भुज के गुण

चूँकि हम पहले ही एक वृत्त में अंकित एक समलम्ब चतुर्भुज के बारे में बात कर चुके हैं, आइए हम इस मुद्दे पर अधिक विस्तार से ध्यान दें। विशेष रूप से, जहां वृत्त का केंद्र समलम्ब के संबंध में है। यहां भी, यह अनुशंसा की जाती है कि हाथ में एक पेंसिल लेने के लिए बहुत आलसी न हों और जो नीचे चर्चा की जाएगी उसे आकर्षित करें। तो आप तेजी से समझेंगे, और बेहतर याद रखेंगे।

1. सर्कल के केंद्र का स्थान ट्रेपेज़ॉइड विकर्ण के पार्श्व पक्ष के झुकाव के कोण से निर्धारित होता है। उदाहरण के लिए, एक विकर्ण समकोण पर समलम्ब के शीर्ष से किनारे तक विस्तारित हो सकता है। इस स्थिति में, बड़ा आधार परिबद्ध वृत्त के केंद्र को बिल्कुल बीच में काटता है (R = ½AE)।
2. विकर्ण और भुजा एक न्यून कोण पर भी मिल सकते हैं - तब वृत्त का केंद्र समलम्ब चतुर्भुज के अंदर होता है।
3. ट्रैपेज़ॉइड विकर्ण और पार्श्व पक्ष के बीच एक अधिक कोण होने पर, परिचालित सर्कल का केंद्र अपने बड़े आधार से परे, ट्रेपेज़ॉइड के बाहर हो सकता है।
4. विकर्ण द्वारा गठित कोण और AKME समलम्बाकार (खुदा हुआ कोण) का बड़ा आधार केंद्रीय कोण का आधा है जो इससे मेल खाता है: एमएई = ½ एमओई.
5. परिचालित वृत्त की त्रिज्या ज्ञात करने के दो तरीकों के बारे में संक्षेप में। विधि एक: अपने चित्र को ध्यान से देखें - आप क्या देखते हैं? आप आसानी से देखेंगे कि विकर्ण समलम्ब को दो त्रिभुजों में विभाजित करता है। त्रिज्या को त्रिभुज की भुजा के विपरीत कोण की ज्या के दो गुणा के अनुपात के रूप में पाया जा सकता है। उदाहरण के लिए, आर = एई / 2 * sinAME... इसी प्रकार, दोनों त्रिभुजों की दोनों भुजाओं के लिए सूत्र लिखा जा सकता है।
6. विधि दो: हम त्रिभुज के त्रिभुज के क्षेत्रफल के माध्यम से परिचालित वृत्त की त्रिज्या पाते हैं, जो समलम्ब चतुर्भुज की भुजा और आधार है: आर = एएम * एमई * एई / 4 * एस एएमई.

एक वृत्त के चारों ओर परिबद्ध एक समलम्ब चतुर्भुज के गुण

यदि एक शर्त पूरी होती है, तो आप एक वृत्त को एक समलम्ब में अंकित कर सकते हैं। इसके बारे में नीचे। और साथ में, आकृतियों के इस संयोजन में कई दिलचस्प गुण हैं।

1. यदि एक वृत्त को समलम्ब चतुर्भुज में अंकित किया जाता है, तो इसकी मध्य रेखा की लंबाई को पक्षों की लंबाई जोड़कर और परिणामी योग को आधे में विभाजित करके आसानी से पाया जा सकता है: एम = (सी + डी) / 2.
2. AKME ट्रेपेज़ॉइड में, एक वृत्त के चारों ओर परिचालित, आधारों की लंबाई का योग पार्श्व पक्षों की लंबाई के योग के बराबर होता है: एके + एमई = केएम + एई.
3. एक समलंब के आधारों के इस गुण से, विपरीत कथन इस प्रकार है: उस समलंब में एक वृत्त अंकित किया जा सकता है, जिसके आधारों का योग पार्श्व भुजाओं के योग के बराबर होता है।
4. ट्रैपेज़ॉइड में अंकित त्रिज्या r के साथ एक वृत्त का स्पर्शरेखा बिंदु पक्ष की ओर को दो खंडों में विभाजित करता है, आइए उन्हें a और b कहते हैं। एक वृत्त की त्रिज्या की गणना सूत्र द्वारा की जा सकती है: आर = ab.
5. और एक और संपत्ति। भ्रमित न होने के लिए, यह उदाहरण स्वयं भी बनाएं। हमारे पास एक अच्छा पुराना AKME ट्रेपेज़ॉइड है जो एक सर्कल के चारों ओर घिरा हुआ है। इसमें विकर्ण खींचे जाते हैं, जो बिंदु O पर प्रतिच्छेद करते हैं।
   इन त्रिभुजों की ऊँचाई, कर्ण (अर्थात, समलम्ब के पार्श्व पक्ष) पर गिराई गई, उत्कीर्ण वृत्त की त्रिज्या के साथ मेल खाती है। और ट्रेपोजॉइड की ऊंचाई खुदे हुए सर्कल के व्यास के साथ मेल खाती है।

आयताकार समलम्बाकार गुण

एक आयताकार ट्रेपोजॉइड कहा जाता है, जिसका एक कोना सही होता है। और इसके गुण इसी परिस्थिति से उपजे हैं।

1. एक आयताकार समलम्ब चतुर्भुज में, पार्श्व पक्षों में से एक आधारों के लंबवत होता है।
2. समलंब की ऊंचाई और पार्श्व पक्ष, समकोण से सटे हुए, समान हैं। यह आपको एक आयताकार समलम्ब चतुर्भुज के क्षेत्रफल की गणना करने की अनुमति देता है (सामान्य सूत्र एस = (ए + बी) * एच / 2) न केवल ऊंचाई के माध्यम से, बल्कि समकोण से सटे पार्श्व पक्ष के माध्यम से भी।
3. एक आयताकार ट्रेपोजॉइड के लिए, ऊपर वर्णित ट्रेपोजॉइड विकर्णों के सामान्य गुण प्रासंगिक हैं।

समलम्ब चतुर्भुज के कुछ गुणों के प्रमाण

समद्विबाहु समलंब के आधार पर कोणों की समानता:

• आप शायद पहले से ही अनुमान लगा चुके हैं कि यहां हमें फिर से एक AKME ट्रेपेज़ॉइड की आवश्यकता है - एक समद्विबाहु ट्रेपोज़ाइड बनाएं। AK (MT || AK) के पार्श्व पक्ष के समानांतर, M के शीर्ष से एक सीधी रेखा MT खींचिए।

परिणामी चतुर्भुज AKMT एक समांतर चतुर्भुज (AK || MT, KM || AT) है। चूँकि ME = KA = MT, MTE समद्विबाहु है और MET = MTE।

एके || एमटी, इसलिए एमटीई = केएई, मेट = एमटीई = केएई।

जहां से AKM = 180 0 - MET = 180 0 - KAE = KME।

क्यू.ई.डी.

अब, एक समद्विबाहु समलम्बाकार (विकर्णों की समानता) के गुण के आधार पर, हम सिद्ध करते हैं कि समलंब AKME समद्विबाहु है:

• आरंभ करने के लिए, आइए एक सीधी रेखा खींचते हैं MX - MX || केई. हम एक समांतर चतुर्भुज KMXE (आधार - MX || KE और KM || EX) प्राप्त करते हैं।

AMX समद्विबाहु है, क्योंकि AM = KE = MX, और MAX = MEA।

एमएक्स || केई, केईए = एमएक्सई, इसलिए एमएई = एमएक्सई।

यह पता चला कि त्रिभुज AKE और EMA एक दूसरे के बराबर हैं, क्योंकि AM = KE और AE दो त्रिभुजों की उभयनिष्ठ भुजा हैं। और एमएई = एमएक्सई भी। हम यह निष्कर्ष निकाल सकते हैं कि AK = ME, और इससे यह निष्कर्ष निकलता है कि AKME समलम्बाकार समद्विबाहु है।

दोहराने के लिए एक कार्य

AKME ट्रेपेज़ॉइड के आधार 9 सेमी और 21 सेमी हैं, अंतरिक्ष यान का पार्श्व पक्ष, 8 सेमी के बराबर, छोटे आधार के साथ 150 0 का कोण बनाता है। समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात करना आवश्यक है।

हल: K के शीर्ष से, हम ऊँचाई को समलम्ब चतुर्भुज के बड़े आधार तक कम करते हैं। और आइए समलम्ब चतुर्भुज के कोनों को देखना शुरू करें।

कोण AEM और KAN एकतरफा हैं। इसका मतलब है कि वे कुल मिलाकर 180 0 देते हैं। इसलिए, KAN = 30 0 (ट्रेपेज़ॉइड कोणों के गुणों के आधार पर)।

अब एक आयताकार ANK पर विचार करें (मुझे लगता है कि यह बिंदु बिना अतिरिक्त सबूत के पाठकों के लिए स्पष्ट है)। इससे हम समलम्ब चतुर्भुज KN की ऊँचाई ज्ञात करते हैं - त्रिभुज में यह पैर है, जो 30 0 के कोण के विपरीत स्थित है। अत: KH = ½AB = 4 सेमी.

समलम्ब चतुर्भुज का क्षेत्रफल सूत्र द्वारा ज्ञात किया जाता है: S AKME = (KM + AE) * KN / 2 = (9 + 21) * 4/2 = 60 सेमी 2।

अंतभाषण

यदि आपने इस लेख का सावधानीपूर्वक और सोच-समझकर अध्ययन किया है, तो उपरोक्त सभी गुणों के लिए एक पेंसिल के साथ ट्रेपेज़ॉइड खींचने और व्यवहार में उन्हें अलग करने के लिए बहुत आलसी नहीं थे, सामग्री को आपके द्वारा अच्छी तरह से समझा जाना चाहिए था।

बेशक, यहां बहुत सारी जानकारी है, विविध और कभी-कभी भ्रमित करने वाली भी: वर्णित ट्रेपोजॉइड के गुणों को खुदा के गुणों के साथ भ्रमित करना इतना मुश्किल नहीं है। लेकिन आपने खुद देखा है कि अंतर बहुत बड़ा है।

अब आपके पास सभी सामान्य समलम्बाकार गुणों की विस्तृत रूपरेखा है। साथ ही समद्विबाहु और आयताकार समलम्ब के विशिष्ट गुण और विशेषताएं। परीक्षण और परीक्षा की तैयारी के लिए उनका उपयोग करना बहुत सुविधाजनक है। इसे स्वयं आज़माएं और अपने दोस्तों के साथ लिंक साझा करें!

साइट, सामग्री की पूर्ण या आंशिक प्रतिलिपि के साथ, स्रोत के लिए एक लिंक आवश्यक है।

एक समलम्ब चतुर्भुज का एक विशेष मामला है जिसमें पक्षों की एक जोड़ी समानांतर होती है। शब्द "ट्रेपेज़ियम" ग्रीक शब्द α से आया है, जिसका अर्थ है "टेबल", "टेबल"। इस लेख में हम ट्रेपोजॉइड के प्रकार और इसके गुणों को देखेंगे। इसके अलावा, हम यह पता लगाएंगे कि इसके अलग-अलग तत्वों की गणना कैसे करें उदाहरण के लिए, एक समद्विबाहु समलम्बाकार का विकर्ण, केंद्र रेखा, क्षेत्र, आदि। सामग्री को प्राथमिक लोकप्रिय ज्यामिति की शैली में प्रस्तुत किया गया है, अर्थात्, में आसानी से सुलभ रूप।

सामान्य जानकारी

सबसे पहले, आइए जानें कि चतुर्भुज क्या है। यह आकृति चार भुजाओं और चार शीर्षों वाले बहुभुज का एक विशेष मामला है। एक चतुर्भुज के दो शीर्ष जो आसन्न नहीं हैं, विपरीत कहलाते हैं। दो गैर-आसन्न पक्षों के लिए भी यही कहा जा सकता है। चतुर्भुज के मुख्य प्रकार समांतर चतुर्भुज, आयत, समचतुर्भुज, वर्ग, समलम्बाकार और त्रिशंकु हैं।

तो, वापस ट्रेपोजॉइड्स पर। जैसा कि हमने कहा, इस आकृति की दो भुजाएँ समानांतर हैं। उन्हें आधार कहा जाता है। अन्य दो (गैर-समानांतर) पक्ष हैं। परीक्षाओं और विभिन्न परीक्षणों की सामग्री में, आप अक्सर ट्रेपेज़ियम से संबंधित कार्य पा सकते हैं, जिसके समाधान के लिए अक्सर छात्र को ज्ञान की आवश्यकता होती है जो कार्यक्रम द्वारा प्रदान नहीं किया जाता है। स्कूल ज्यामिति पाठ्यक्रम छात्रों को कोणों और विकर्णों के गुणों के साथ-साथ एक समद्विबाहु समलंब की मध्य रेखा से परिचित कराता है। लेकिन इसके अलावा, उल्लिखित ज्यामितीय आकृति में अन्य विशेषताएं हैं। लेकिन उनके बारे में थोड़ी देर बाद...

ट्रेपोजॉइड के प्रकार

यह आकृति कई प्रकार की होती है। हालांकि, अक्सर उनमें से दो पर विचार करने की प्रथा है - समद्विबाहु और आयताकार।

1. एक आयताकार समलम्ब चतुर्भुज एक आकृति है जिसमें एक पार्श्व भुजा आधारों के लंबवत होती है। इसके दो कोण सदैव नब्बे अंश के बराबर होते हैं।

2. एक समद्विबाहु समलम्ब एक ज्यामितीय आकृति है जिसकी भुजाएँ एक दूसरे के बराबर होती हैं। इसका मतलब यह है कि आधारों पर कोण भी जोड़ीदार बराबर होते हैं।

ट्रेपेज़ॉइड के गुणों के अध्ययन के लिए कार्यप्रणाली के मुख्य सिद्धांत

मुख्य सिद्धांत तथाकथित कार्य दृष्टिकोण का उपयोग है। वास्तव में, इस आकृति के नए गुणों को ज्यामिति के सैद्धांतिक पाठ्यक्रम में शामिल करने की कोई आवश्यकता नहीं है। उन्हें विभिन्न समस्याओं (सिस्टम वाले से बेहतर) को हल करने की प्रक्रिया में खोला और तैयार किया जा सकता है। साथ ही, यह बहुत महत्वपूर्ण है कि शिक्षक यह जानता है कि स्कूली बच्चों को शैक्षिक प्रक्रिया में एक बिंदु या किसी अन्य पर कौन से कार्य दिए जाने की आवश्यकता है। इसके अलावा, प्रत्येक ट्रेपोजॉइड संपत्ति को कार्य प्रणाली में एक महत्वपूर्ण कार्य के रूप में दर्शाया जा सकता है।

दूसरा सिद्धांत ट्रेपेज़ॉइड के "उल्लेखनीय" गुणों के अध्ययन का तथाकथित सर्पिल संगठन है। इसका तात्पर्य किसी दिए गए ज्यामितीय आकृति की व्यक्तिगत विशेषताओं के लिए सीखने की प्रक्रिया में वापसी है। इससे शिक्षार्थियों के लिए उन्हें याद करना आसान हो जाता है। उदाहरण के लिए, चार बिंदुओं की संपत्ति। यह समानता का अध्ययन करके और बाद में सदिशों का उपयोग करके दोनों को सिद्ध किया जा सकता है। और आकृति की पार्श्व भुजाओं से सटे त्रिभुजों के समान आकार को न केवल एक सीधी रेखा पर स्थित भुजाओं पर खींची गई समान ऊँचाई वाले त्रिभुजों के गुणों को लागू करके सिद्ध किया जा सकता है, बल्कि सूत्र S = 1/2 का उपयोग करके भी सिद्ध किया जा सकता है। (अब * sinα)। इसके अलावा, आप एक वर्णित ट्रेपोजॉइड, आदि पर एक खुदा हुआ ट्रेपोजॉइड या एक समकोण त्रिभुज पर काम कर सकते हैं।

एक स्कूल पाठ्यक्रम की सामग्री में एक ज्यामितीय आकृति की "अतिरिक्त पाठ्यचर्या" सुविधाओं का उपयोग उन्हें पढ़ाने के लिए एक कार्य तकनीक है। अन्य विषयों को पास करते समय अध्ययन किए गए गुणों के लिए लगातार अपील छात्रों को ट्रेपोजॉइड की गहरी समझ हासिल करने की अनुमति देती है और असाइन किए गए कार्यों को हल करने की सफलता सुनिश्चित करती है। तो, आइए इस अद्भुत आकृति का अध्ययन करने के लिए नीचे उतरें।

समद्विबाहु समलम्बाकार के तत्व और गुण

जैसा कि हमने पहले ही नोट किया है, इस ज्यामितीय आकृति की भुजाएँ समान हैं। इसे एक नियमित ट्रेपोजॉइड के रूप में भी जाना जाता है। और यह इतना उल्लेखनीय क्यों है और इसे ऐसा नाम क्यों मिला? इस आकृति की ख़ासियत में यह तथ्य शामिल है कि इसके न केवल आधारों पर भुजाएँ और कोण हैं, बल्कि विकर्ण भी हैं। इसके अलावा, समद्विबाहु समलंब के कोणों का योग 360 डिग्री होता है। लेकिन वह सब नहीं है! सभी ज्ञात समलंबों में से केवल एक समद्विबाहु के चारों ओर एक वृत्त का वर्णन किया जा सकता है। यह इस तथ्य के कारण है कि इस आकृति के विपरीत कोणों का योग 180 डिग्री है, और केवल इस शर्त के तहत एक चतुर्भुज के चारों ओर एक चक्र का वर्णन किया जा सकता है। माना ज्यामितीय आकृति की अगली संपत्ति यह है कि आधार के शीर्ष से विपरीत शीर्ष के प्रक्षेपण तक की दूरी जिसमें यह आधार शामिल है, केंद्र रेखा के बराबर होगी।

अब आइए जानें कि समद्विबाहु समलम्बाकार के कोण कैसे ज्ञात करें। इस समस्या के समाधान पर विचार करें, बशर्ते कि आकृति के पक्षों के आयाम ज्ञात हों।

समाधान

आमतौर पर, चतुर्भुज को आमतौर पर ए, बी, सी, डी अक्षरों से दर्शाया जाता है, जहां बीएस और एडी आधार होते हैं। एक समद्विबाहु समलम्ब में भुजाएँ बराबर होती हैं। हम मानेंगे कि उनका आकार X के बराबर है, और आधारों का आकार Y और Z के बराबर है (क्रमशः छोटा और बड़ा)। गणना करने के लिए, कोण B से ऊँचाई H खींचना आवश्यक है। परिणाम एक समकोण त्रिभुज ABN है, जहाँ AB कर्ण है, और BN और AN पैर हैं। हम पैर एएच के आकार की गणना करते हैं: बड़े आधार से छोटे को घटाएं, और परिणाम को 2 से विभाजित करें। हम इसे सूत्र के रूप में लिखते हैं: (जेडवाई) / 2 = एफ। अब, तीव्र कोण की गणना करने के लिए त्रिभुज के लिए, हम cos फ़ंक्शन का उपयोग करते हैं। हमें निम्नलिखित रिकॉर्ड मिलते हैं: cos (β) = X / F। अब हम कोण की गणना करते हैं: β = आर्कोस (एक्स / एफ)। इसके अलावा, एक कोण को जानकर, हम दूसरे को निर्धारित कर सकते हैं, इसके लिए हम एक प्राथमिक अंकगणितीय ऑपरेशन करते हैं: 180 - β। सभी कोण परिभाषित हैं।

इस समस्या का दूसरा समाधान भी है। शुरुआत में, हम कोने से एन की ऊंचाई कम करते हैं। पैर बीएन के मूल्य की गणना करें। हम जानते हैं कि एक समकोण त्रिभुज के कर्ण का वर्ग पैरों के वर्गों के योग के बराबर होता है। हम पाते हैं: बीएन = (एक्स 2-एफ 2)। इसके बाद, हम त्रिकोणमितीय फलन tg का उपयोग करते हैं। नतीजतन, हमारे पास है: β = आर्कटन (बीएन / एफ)। एक नुकीला कोना मिला है। इसके अलावा, हम उसी तरह परिभाषित करते हैं जैसे पहली विधि में।

समद्विबाहु समलम्ब चतुर्भुज के विकर्णों का गुण

सबसे पहले, आइए चार नियम लिखें। यदि एक समद्विबाहु समलम्ब में विकर्ण लंबवत हैं, तो:

आकृति की ऊंचाई दो से विभाजित आधारों के योग के बराबर होगी;

इसकी ऊंचाई और मध्य रेखा बराबर हैं;

वृत्त का केंद्र वह बिंदु है जिस पर वे प्रतिच्छेद करते हैं;

यदि पार्श्व पक्ष को स्पर्शरेखा के बिंदु से खंड H और M में विभाजित किया जाता है, तो यह इन खंडों के गुणनफल के वर्गमूल के बराबर होता है;

चतुर्भुज, जो संपर्क के बिंदुओं, समलम्ब चतुर्भुज के शीर्ष और खुदे हुए वृत्त के केंद्र से बनता है, एक वर्ग है जिसकी भुजा त्रिज्या के बराबर होती है;

आकृति का क्षेत्रफल आधारों के गुणनफल और आधारों के आधे योग के गुणनफल के बराबर होता है।

समान समलम्ब चतुर्भुज

इस विषय के गुणों का अध्ययन करने के लिए यह विषय बहुत सुविधाजनक है। उदाहरण के लिए, विकर्ण समलंब चतुर्भुज को चार त्रिभुजों में विभाजित करते हैं, और जो आधारों से सटे होते हैं वे समान होते हैं, और पार्श्व भुजाएँ समान होती हैं। इस कथन को त्रिभुजों का एक गुण कहा जा सकता है जिसमें एक समलम्ब को उसके विकर्णों द्वारा विभाजित किया जाता है। इस कथन का पहला भाग दो कोणों में समानता के चिन्ह से सिद्ध होता है। दूसरे भाग को सिद्ध करने के लिए, नीचे दी गई विधि का उपयोग करना बेहतर है।

प्रमेय का प्रमाण

हम स्वीकार करते हैं कि एबीएसडी (बीपी और बीएस समलम्बाकार के आधार हैं) का आंकड़ा वीडी और एएस के विकर्णों से विभाजित है। उनके चौराहे का बिंदु ओ है। हमें चार त्रिकोण मिलते हैं: एओएस - निचले आधार पर, बीओएस - ऊपरी आधार पर, एबीओ और एसओडी पार्श्व पक्षों पर। यदि खंड BO और OD उनके आधार हैं, तो त्रिभुज SOD और BFB की ऊँचाई समान होती है। हम पाते हैं कि उनके क्षेत्रों (पी) के बीच का अंतर इन खंडों के बीच के अंतर के बराबर है: पीबीओएस / पीएसओडी = बीओ / ओडी = के। इसलिए, पीएसओडी = पीबीओएस / के। इसी तरह, त्रिभुज BFB और AOB की ऊंचाई समान होती है। हम खंडों SB और OA को उनके आधारों के लिए लेते हैं। हमें PBOS / PAOB = SO / OA = K और PAOB = PBOS / K मिलता है। इससे यह पता चलता है कि PSOD = PAOB।

सामग्री को समेकित करने के लिए, छात्रों को सलाह दी जाती है कि वे परिणामी त्रिभुजों के क्षेत्रों के बीच एक संबंध खोजें, जिसमें समलम्ब चतुर्भुज को इसके विकर्णों द्वारा विभाजित किया जाता है, जिससे निम्नलिखित समस्या का समाधान होता है। यह ज्ञात है कि बायोफीडबैक और एओडी त्रिकोण के क्षेत्र समान हैं, समलम्बाकार क्षेत्र का पता लगाना आवश्यक है। चूँकि PSOD = PAOB, इसका अर्थ है कि PABSD = PBOS + PAOD + 2 * PSOD। त्रिभुज BFB और AOD की समानता से यह निम्नानुसार है कि BO / OD = (PBOS / PAOD)। इसलिए, PBOS / PSOD = BO / OD = (PBOS / PAOD)। हमें PSOD = (PBOS * PAOD) मिलता है। तब PABSD = PBOS + PAOD + 2 * (PBOS * PAOD) = (√ PSOS + PAOD) 2.

समानता गुण

इस विषय को विकसित करना जारी रखते हुए, आप ट्रेपेज़ॉइड की अन्य दिलचस्प विशेषताओं को साबित कर सकते हैं। तो, समानता की मदद से, कोई एक खंड की संपत्ति को साबित कर सकता है जो इस ज्यामितीय आकृति के विकर्णों के चौराहे द्वारा गठित एक बिंदु से होकर गुजरता है, जो आधारों के समानांतर है। ऐसा करने के लिए, हम निम्नलिखित समस्या को हल करेंगे: खंड RK की लंबाई ज्ञात करना आवश्यक है, जो बिंदु O से होकर गुजरता है। त्रिभुज AOD और BFB की समानता से, यह इस प्रकार है कि AO / OS = AD / BS . त्रिभुज AOR और ASB की समानता से, यह इस प्रकार है कि AO / AC = RO / BS = HELL / (BS + HELL)। यहाँ से हमें वह RO = BS * HELL / (BS + HELL) मिलता है। इसी तरह, त्रिभुज DOK और DBS की समानता से, यह निम्नानुसार है कि OK = BS * HELL / (BS + HELL)। यहाँ से हम पाते हैं कि RO = OK और RK = 2 * BS * HELL / (BS + HELL)। आधारों के समानांतर और दोनों पक्षों को जोड़ने वाले विकर्णों के प्रतिच्छेदन बिंदु से गुजरने वाले खंड को प्रतिच्छेदन बिंदु से आधा कर दिया जाता है। इसकी लंबाई आकृति के आधार का हार्मोनिक माध्य है।

निम्नलिखित समलम्बाकार गुण पर विचार करें, जिसे चार सूत्री गुण कहते हैं। विकर्णों (ओ) के चौराहे के बिंदु, पार्श्व पक्षों (ई) के विस्तार के चौराहे के साथ-साथ आधारों के मध्य बिंदु (टी और जी) हमेशा एक ही रेखा पर स्थित होते हैं। यह समानता की विधि से आसानी से सिद्ध हो जाता है। परिणामी त्रिभुज BES और AED समान हैं, और उनमें से प्रत्येक में माध्यिकाएँ ET और EZ शीर्ष E पर कोण को बराबर भागों में विभाजित करती हैं। नतीजतन, बिंदु E, T और Ж एक सीधी रेखा पर स्थित हैं। इसी तरह, बिंदु T, O, और Z एक सीधी रेखा पर स्थित हैं। यह सब त्रिभुज BFB और AOD की समानता से होता है। इससे हम यह निष्कर्ष निकालते हैं कि सभी चार बिंदु - E, T, O और F - एक सीधी रेखा पर स्थित होंगे।

ऐसे समलंबों का उपयोग करके, आप विद्यार्थियों से उस खंड (LF) की लंबाई ज्ञात करने के लिए कह सकते हैं जो आकृति को दो समान भागों में विभाजित करता है। यह खंड आधारों के समानांतर होना चाहिए। चूंकि प्राप्त समलम्ब ALPD और LBSF समान हैं, तो BS / LF = LF / BP। यह इस प्रकार है कि LF = (BS * HELL)। हम पाते हैं कि समलम्ब चतुर्भुज को दो समान भागों में विभाजित करने वाले खंड की लंबाई आकृति के आधारों की लंबाई के ज्यामितीय माध्य के बराबर होती है।

निम्नलिखित समानता संपत्ति पर विचार करें। यह एक खंड पर आधारित है जो समलम्ब को दो समान आकार के आंकड़ों में विभाजित करता है। हम मानते हैं कि ABSD समलम्बाकार खंड द्वारा दो समान भागों में विभाजित है। शीर्ष बी से, ऊंचाई गिरा दी जाती है, जिसे खंड ईएच द्वारा दो भागों - बी 1 और बी 2 में विभाजित किया जाता है। हम प्राप्त करते हैं: पीएबीएसडी/2 = (बीएस + ईएच) * बी 1/2 = (हेल + ईएच) * बी 2/2 और पीएबीएसडी = (बीएस + एचईएल) * (बी 1 + बी 2)/2। इसके बाद, हम एक प्रणाली की रचना करते हैं, जिसका पहला समीकरण (BS + EH) * B1 = (HELL + EH) * B2 और दूसरा (BS + EH) * B1 = (BS + HELL) * (B1 + B2) है। / २. यह इस प्रकार है कि B2 / B1 = (BS + EH) / (HELL + EH) और BS + EH = ((BS + HELL) / 2) * (1 + B2 / B1)। हम पाते हैं कि समलम्ब चतुर्भुज को दो समान आकारों में विभाजित करने वाले खंड की लंबाई आधारों की लंबाई के मूल माध्य वर्ग के बराबर होती है: ((BS2 + AD2) / 2)।

समानता निष्कर्ष

इस प्रकार, हमने साबित कर दिया है कि:

1. समलम्ब पर पार्श्व पक्षों के मध्य बिंदुओं को जोड़ने वाला खंड बीपी और बीएस के समानांतर है और बीएस और बीपी के अंकगणितीय माध्य (ट्रेपेज़ॉइड के आधार की लंबाई) के बराबर है।

2. HELL और BS के समानांतर विकर्णों के प्रतिच्छेदन के बिंदु O से गुजरने वाली रेखा HELL और BS (2 * BS * HELL / (BS + HELL)) की संख्याओं के हार्मोनिक माध्य के बराबर होगी।

3. समलम्ब को समान भागों में विभाजित करने वाले खंड में BS और HELL के आधारों के ज्यामितीय माध्य की लंबाई होती है।

4. आकृति को दो समान आकारों में विभाजित करने वाले तत्व की लंबाई BP और BS के माध्य वर्ग संख्याओं की होती है।

सामग्री को समेकित करने और विचार किए गए खंडों के बीच संबंध को समझने के लिए, छात्र को उन्हें एक विशिष्ट समलम्बाकार के लिए बनाने की आवश्यकता है। वह आसानी से मध्य रेखा और उस खंड को प्रदर्शित कर सकता है जो बिंदु O से होकर गुजरता है - आकृति के विकर्णों का प्रतिच्छेदन - आधारों के समानांतर। लेकिन तीसरा और चौथा कहाँ स्थित होगा? यह उत्तर छात्र को औसत के बीच वांछित संबंध की खोज करने के लिए प्रेरित करेगा।

समलम्ब चतुर्भुज विकर्णों के मध्य बिंदुओं को जोड़ने वाला खंड

इस आकृति की निम्नलिखित संपत्ति पर विचार करें। हम मानते हैं कि खंड MH आधारों के समानांतर है और विकर्णों को आधा में विभाजित करता है। चौराहे के बिंदु Ш और कहलाएंगे। यह खंड आधारों के आधे अंतर के बराबर होगा। आइए इस पर करीब से नज़र डालते हैं। एमएसएच - एबीएस त्रिकोण की मध्य रेखा, यह बीएस/2 के बराबर है। एमसीएच एबीडी त्रिकोण की मध्य रेखा है, यह बीपी/2 के बराबर है। तब हम पाते हैं कि SHSH = MSH-MSH, इसलिए, SHSH = HELL/2-BS/2 = (HELL + VS)/2.

गुरुत्वाकर्षण का केंद्र

आइए देखें कि किसी दिए गए ज्यामितीय आकृति के लिए इस तत्व को कैसे परिभाषित किया जाता है। ऐसा करने के लिए, आधारों को विपरीत दिशाओं में विस्तारित करना आवश्यक है। इसका क्या मतलब है? निचले एक को ऊपरी आधार पर जोड़ना आवश्यक है - दोनों तरफ, उदाहरण के लिए, दाईं ओर। और निचले वाले को ऊपर वाले की लंबाई से बाईं ओर बढ़ाएं। अगला, हम उन्हें एक विकर्ण के साथ जोड़ते हैं। आकृति की मध्य रेखा के साथ इस खंड का प्रतिच्छेदन बिंदु समलम्ब चतुर्भुज के गुरुत्वाकर्षण का केंद्र है।

अंकित और वर्णित समलम्बाकार

आइए ऐसी आकृतियों की विशेषताओं को सूचीबद्ध करें:

1. एक समलम्ब चतुर्भुज को एक वृत्त में तभी अंकित किया जा सकता है जब वह समद्विबाहु हो।

2. एक समलम्ब चतुर्भुज को एक वृत्त के चारों ओर वर्णित किया जा सकता है, बशर्ते कि उनके आधारों की लंबाई का योग पार्श्व पक्षों की लंबाई के योग के बराबर हो।

अंकित सर्कल परिणाम:

1. वर्णित समलंब की ऊंचाई हमेशा दो त्रिज्या के बराबर होती है।

2. वर्णित समलम्बाकार का पार्श्व पक्ष वृत्त के केंद्र से समकोण पर देखा जाता है।

पहला परिणाम स्पष्ट है, लेकिन दूसरे को साबित करने के लिए यह स्थापित करना आवश्यक है कि एसओडी का कोण सही है, जो वास्तव में मुश्किल भी नहीं होगा। लेकिन इस गुण का ज्ञान आपको समस्याओं को हल करते समय एक समकोण त्रिभुज का उपयोग करने की अनुमति देगा।

आइए अब हम एक वृत्त में अंकित समद्विबाहु समलम्बाकार के लिए इन परिणामों को संक्षिप्त करते हैं। हम पाते हैं कि ऊँचाई आकृति के आधार का ज्यामितीय माध्य है: H = 2R = (BS * HELL)। समलम्बाकार (दो ऊंचाइयों को धारण करने का सिद्धांत) के लिए समस्याओं को हल करने की बुनियादी तकनीक का अभ्यास करते समय, छात्र को निम्नलिखित कार्य को हल करना चाहिए। हम मानते हैं कि बीटी एबीएसडी के समद्विबाहु आकृति की ऊंचाई है। एटी और टीडी खंडों को खोजना आवश्यक है। ऊपर वर्णित सूत्र का उपयोग करते हुए, ऐसा करना कठिन नहीं होगा।

अब आइए जानें कि वर्णित ट्रेपोजॉइड के क्षेत्र का उपयोग करके एक वृत्त की त्रिज्या कैसे निर्धारित की जाए। हम ऊंचाई को शीर्ष B से HELL के आधार तक कम करते हैं। चूँकि वृत्त समलम्ब चतुर्भुज में अंकित है, तो BS + HELL = 2AB या AB = (BS + HELL)/2. त्रिभुज ABN से हम sinα = BN / AB = 2 * BN / (BS + HELL) पाते हैं। पीएबीएसडी = (बीएस + एचईएल) * बीएन/2, बीएन = 2आर। हमें पीएबीएसडी = (बीएस + एचईएल) * आर मिलता है, यह इस प्रकार है कि आर = पीएबीएसडी / (बीएस + एचईएल)।

समलम्ब चतुर्भुज की मध्य रेखा के लिए सभी सूत्र

अब इस ज्यामितीय आकार के अंतिम तत्व पर जाने का समय आ गया है। आइए जानें कि समलम्बाकार (M) की मध्य रेखा क्या है:

1. आधारों के माध्यम से: एम = (ए + बी) / 2।

2. ऊंचाई, आधार और कोनों के माध्यम से:

एम = ए-एच * (सीटीजीα + सीटीजीबी) / 2;

एम = बी + एच * (सीटीजीα + सीटीजीबी) / 2।

3. ऊंचाई, विकर्णों और उनके बीच के कोण के माध्यम से। उदाहरण के लिए, D1 और D2 एक समलम्ब चतुर्भुज के विकर्ण हैं; α, β - उनके बीच के कोण:

एम = डी 1 * डी 2 * पाप α / 2 एच = डी 1 * डी 2 * पापβ / 2 एच।

4. क्षेत्र और ऊंचाई के माध्यम से: एम = पी / एन।

परिचालित वृत्त और समलम्बाकार। नमस्कार! आपके लिए एक और प्रकाशन जिसमें हम समलंबों की समस्याओं पर विचार करेंगे। गणित की परीक्षा में कार्य शामिल हैं। यहां उन्हें एक समूह में जोड़ा जाता है, न केवल एक ट्रेपोजॉइड दिया जाता है, बल्कि निकायों का एक संयोजन - एक ट्रेपोजॉइड और एक सर्कल। इनमें से अधिकांश समस्याओं का समाधान मौखिक रूप से किया जाता है। लेकिन कुछ ऐसे भी हैं जिन पर विशेष ध्यान देने की आवश्यकता है, उदाहरण के लिए, कार्य 27926।

आपको कौन सा सिद्धांत याद रखना चाहिए? यह:

ट्रेपेज़ियम की समस्या जो ब्लॉग पर उपलब्ध है, देखी जा सकती है यहां.

27924. समलम्ब चतुर्भुज के चारों ओर एक वृत्त का वर्णन किया गया है। समलम्ब चतुर्भुज का परिमाप 22 है, मध्य रेखा 5 है। समलम्ब चतुर्भुज की भुजा ज्ञात कीजिए।

ध्यान दें कि आप केवल समद्विबाहु समलम्बाकार के चारों ओर एक वृत्त का वर्णन कर सकते हैं। हमें मध्य रेखा दी गई है, जिसका अर्थ है कि हम आधारों का योग निर्धारित कर सकते हैं, अर्थात्:

तो भुजाओं का योग 22–10 = 12 (परिधि घटा आधार) होगा। चूँकि एक समद्विबाहु समलम्ब चतुर्भुज की भुजाएँ बराबर होती हैं, इसलिए एक भुजा छह के बराबर होगी।

27925. एक समद्विबाहु समलम्ब चतुर्भुज का पार्श्व पक्ष उसके छोटे आधार के बराबर है, आधार पर कोण 60 0 है, बड़ा आधार 12 है। इस समलंब के परिबद्ध वृत्त की त्रिज्या ज्ञात कीजिए।

यदि आपने एक वृत्त और उसमें अंकित एक षट्भुज के साथ समस्याओं को हल किया है, तो तुरंत उत्तर दें - त्रिज्या 6 है। क्यों?

देखो: एक समद्विबाहु समलम्बाकार आधार पर कोण 60 0 और बराबर भुजाओं AD, DC और CB के साथ, एक नियमित षट्भुज का आधा है:

ऐसे षट्भुज में, विपरीत शीर्षों को जोड़ने वाला खंड वृत्त के केंद्र से होकर गुजरता है। * षट्भुज का केंद्र और वृत्त का केंद्र समान है, अधिक विवरण

अर्थात्, इस समलम्ब चतुर्भुज का बड़ा आधार परिबद्ध वृत्त के व्यास के साथ मेल खाता है। इस प्रकार, त्रिज्या छह है।

* बेशक, आप त्रिभुज ADO, DOC और OCB की समानता पर विचार कर सकते हैं। सिद्ध कीजिए कि वे समबाहु हैं। इसके अलावा, हम यह निष्कर्ष निकालते हैं कि कोण AOB 180 0 है और बिंदु O शीर्षों A, D, C और B से समान दूरी पर है, और इसलिए AO = OB = 12/2 = 6।

27926. एक समद्विबाहु समलम्ब चतुर्भुज के आधार 8 और 6 हैं। परिबद्ध वृत्त की त्रिज्या 5 है। समलम्ब चतुर्भुज की ऊँचाई ज्ञात कीजिए।

ध्यान दें कि परिबद्ध वृत्त का केंद्र समरूपता की धुरी पर स्थित है, और यदि आप इस केंद्र से गुजरने वाले एक समलंब की ऊंचाई का निर्माण करते हैं, तो जब यह आधारों के साथ प्रतिच्छेद करता है, तो यह उन्हें आधे में विभाजित कर देगा। आइए इसे स्केच में दिखाते हैं, केंद्र को कोने से भी जोड़ते हैं:

खंड ईएफ समलम्बाकार की ऊंचाई है, हमें इसे खोजने की जरूरत है।

समकोण त्रिभुज OFC में, हम कर्ण (यह वृत्त की त्रिज्या है), FC = 3 (क्योंकि DF = FC) जानते हैं। पाइथागोरस प्रमेय द्वारा, हम OF की गणना कर सकते हैं:

समकोण त्रिभुज OEB में, हम कर्ण (यह वृत्त की त्रिज्या है), EB = 4 (क्योंकि AE = EB) जानते हैं। पाइथागोरस प्रमेय द्वारा, हम OE की गणना कर सकते हैं:

तो ईएफ = एफओ + ओई = 4 + 3 = 7।

अब एक महत्वपूर्ण बारीकियाँ!

इस समस्या में, आकृति स्पष्ट रूप से दिखाती है कि आधार वृत्त के केंद्र के विपरीत पक्षों पर स्थित हैं, इसलिए समस्या इस तरह हल हो जाती है।

और क्या होगा अगर हालत में एक स्केच नहीं दिया गया था?

तब समस्या के दो उत्तर होंगे। क्यों? ध्यान से देखें - आप किसी भी सर्कल में दिए गए आधारों के साथ दो ट्रैपेज़ॉयड लिख सकते हैं:

* अर्थात्, समलंब का आधार और वृत्त की त्रिज्या को देखते हुए, दो समलंब होते हैं।

और निर्णय "दूसरा विकल्प" इस प्रकार होगा।

पाइथागोरस प्रमेय द्वारा, हम की गणना करते हैं:

आइए OE की गणना भी करें:

इस प्रकार, EF = FO - OE = 4–3 = 1।

बेशक, परीक्षा के संक्षिप्त उत्तर के साथ एक समस्या में, दो उत्तर नहीं हो सकते हैं, और ऐसी समस्या बिना स्केच के नहीं दी जाएगी। इसलिए स्केच पर विशेष ध्यान दें! अर्थात्: ट्रेपेज़ॉइड के आधार कैसे स्थित हैं। लेकिन विस्तृत उत्तर वाले कार्यों में, यह पिछले वर्षों में (थोड़ी जटिल स्थिति के साथ) मौजूद था। जो कोई भी ट्रेपेज़ॉइड के स्थान के लिए केवल एक विकल्प पर विचार करता है, वह इस कार्य पर बिंदु खो देता है।

27937. वृत्त के चारों ओर एक समलम्ब का वर्णन किया गया है, जिसका परिमाप 40 है। इसकी केंद्र रेखा ज्ञात कीजिए।

यहां आपको एक वृत्त के चारों ओर परिबद्ध चतुर्भुज का गुण तुरंत याद करना चाहिए:

किसी वृत्त के चारों ओर परिबद्ध किसी चतुर्भुज की सम्मुख भुजाओं का योग बराबर होता है।

1. समलम्ब चतुर्भुज विकर्णों के मध्य बिंदुओं को जोड़ने वाला खंड आधार अंतर के आधे के बराबर है
2. समलम्ब चतुर्भुज के आधारों और विकर्णों के खंडों से उनके प्रतिच्छेदन बिंदु तक बनने वाले त्रिभुज समान होते हैं
3. समलम्ब चतुर्भुज के विकर्णों के खंडों द्वारा गठित त्रिभुज, जिसके किनारे समलम्बाकार के पार्श्व पक्षों पर स्थित होते हैं - समान (समान क्षेत्र होते हैं)
4. यदि आप समलम्ब चतुर्भुज के पार्श्व पक्षों को छोटे आधार की ओर बढ़ाते हैं, तो वे आधारों के मध्य बिंदुओं को जोड़ने वाली सीधी रेखा के साथ एक बिंदु पर प्रतिच्छेद करते हैं
5. ट्रेपेज़ॉइड के आधारों को जोड़ने वाले और ट्रेपोज़ॉइड के विकर्णों के चौराहे के बिंदु से गुजरने वाले खंड को इस बिंदु से ट्रेपोज़ॉइड के आधारों की लंबाई के अनुपात के बराबर अनुपात में विभाजित किया जाता है।
6. ट्रेपेज़ॉइड के आधार के समानांतर और विकर्णों के चौराहे के बिंदु के माध्यम से खींचा गया एक खंड इस बिंदु से आधे में विभाजित होता है, और इसकी लंबाई 2ab / (a ​​+ b) के बराबर होती है, जहां a और b आधार होते हैं समलम्ब चतुर्भुज का

समलम्ब चतुर्भुज विकर्णों के मध्य बिंदुओं को जोड़ने वाले रेखाखंड के गुण

हम समलम्ब चतुर्भुज ABCD के विकर्णों के मध्य बिंदुओं को जोड़ते हैं, जिसके परिणामस्वरूप हमारे पास एक खंड LM है।
समलम्ब चतुर्भुज विकर्णों के मध्य बिंदुओं को जोड़ने वाला खंड, समलम्ब चतुर्भुज की मध्य रेखा पर स्थित है.

यह खंड समलम्ब चतुर्भुज के आधारों के समानांतर.

समलम्ब चतुर्भुज के विकर्णों के मध्य बिंदुओं को जोड़ने वाले खंड की लंबाई इसके आधारों के आधे अंतर के बराबर होती है।

एलएम = (एडी - बीसी) / 2
या
एलएम = (ए-बी) / 2

समलम्ब चतुर्भुज के विकर्णों से बने त्रिभुजों के गुण

समलम्ब चतुर्भुज के आधारों और समलम्ब चतुर्भुज के विकर्णों के प्रतिच्छेदन बिंदु से बनने वाले त्रिभुज - समान है.
त्रिभुज BOC और AOD समान हैं। चूँकि कोण BOC और AOD लंबवत हैं, वे बराबर हैं।
कोण OCB और OAD समानांतर रेखा AD और BC के साथ आंतरिक क्रॉसवाइज हैं (ट्रेपेज़ॉइड के आधार एक दूसरे के समानांतर हैं) और छेदक रेखा AC, इसलिए, वे समान हैं।
कोण ओबीसी और ओडीए एक ही कारण (आंतरिक क्रॉस-क्रॉसिंग) के बराबर हैं।

चूँकि एक त्रिभुज के तीनों कोण दूसरे त्रिभुज के संगत कोणों के बराबर होते हैं, इसलिए ये त्रिभुज समरूप होते हैं।

इससे क्या होता है?

ज्यामिति में समस्याओं को हल करने के लिए त्रिभुजों की समरूपता का प्रयोग इस प्रकार किया जाता है। यदि हम समरूप त्रिभुजों के दो संगत तत्वों की लंबाई का मान जानते हैं, तो हम समानता का गुणांक पाते हैं (हम एक को दूसरे से विभाजित करते हैं)। जहां से अन्य सभी तत्वों की लंबाई एक दूसरे से बिल्कुल समान मूल्य के साथ संबंधित है।

समलम्ब चतुर्भुज की भुजाओं और विकर्णों पर स्थित त्रिभुजों के गुण

समलम्ब चतुर्भुज AB और CD के पार्श्व पक्षों पर स्थित दो त्रिभुजों पर विचार करें। ये त्रिभुज AOB और COD हैं। इस तथ्य के बावजूद कि इन त्रिभुजों के अलग-अलग पक्षों के आकार पूरी तरह से भिन्न हो सकते हैं, लेकिन पक्षों द्वारा गठित त्रिभुजों के क्षेत्रफल और समलम्ब चतुर्भुज के विकर्णों के प्रतिच्छेदन बिंदु हैंअर्थात् त्रिभुजों का आकार बराबर होता है।

यदि आप समलम्ब चतुर्भुज की भुजाओं को छोटे आधार की ओर बढ़ाते हैं, तो भुजाओं का प्रतिच्छेदन बिंदु होगा आधारों के मध्यबिंदुओं से होकर जाने वाली एक सीधी रेखा से सुमेलित करें.

इस प्रकार, किसी भी समलम्ब को त्रिभुज तक बढ़ाया जा सकता है। जिसमें:

• विस्तारित पार्श्व पक्षों के चौराहे पर एक सामान्य शीर्ष के साथ एक समलम्ब चतुर्भुज के आधारों द्वारा गठित त्रिभुज समान होते हैं
• समलम्ब चतुर्भुज के आधारों के मध्य बिंदुओं को जोड़ने वाली सीधी रेखा, उसी समय, निर्मित त्रिभुज की माध्यिका होती है।

समलम्बाकार आधारों को जोड़ने वाली रेखा के गुण

यदि आप एक खंड खींचते हैं, जिसके सिरे समलम्ब चतुर्भुज के आधारों पर स्थित होते हैं, जो समलम्ब चतुर्भुज (KN) के विकर्णों के प्रतिच्छेदन बिंदु पर स्थित होता है, तो आधार के किनारे से इसके घटक खंडों का अनुपात विकर्णों का प्रतिच्छेदन बिंदु (KO / ON) समलम्ब चतुर्भुज के आधारों के अनुपात के बराबर होगा(ईसा पूर्व/ई.)

KO / ON = BC / AD

यह गुण संगत त्रिभुजों (ऊपर देखें) की समानता से अनुसरण करता है।

समलम्ब चतुर्भुज के आधारों के समानांतर एक रेखा के गुण

यदि आप समलम्ब चतुर्भुज के आधारों के समानांतर एक खंड खींचते हैं और समलम्ब चतुर्भुज के विकर्णों के प्रतिच्छेदन बिंदु से गुजरते हैं, तो इसमें निम्नलिखित गुण होंगे:

• प्रीसेट दूरी (किमी) समलम्ब चतुर्भुज विकर्णों के प्रतिच्छेदन बिंदु को आधे में विभाजित करता है
• खंड की लंबाईसमलम्ब चतुर्भुज के विकर्णों के प्रतिच्छेदन बिंदु से गुजरना और आधारों के समानांतर बराबर है केएम = 2ab / (ए + बी)

समलम्ब चतुर्भुज के विकर्ण ज्ञात करने के सूत्र

ए, बी- समलम्ब चतुर्भुज का आधार

सी, डी- समलम्ब चतुर्भुज के पार्श्व पक्ष

d1 d2- समलम्ब चतुर्भुज विकर्ण

α β - समलम्ब चतुर्भुज के बड़े आधार वाले कोण

आधार पर आधारों, भुजाओं और कोणों के माध्यम से एक समलम्ब चतुर्भुज के विकर्णों को खोजने के सूत्र

सूत्रों का पहला समूह (1-3) समलम्बाकार विकर्णों के मुख्य गुणों में से एक को दर्शाता है:

1. एक समलम्ब चतुर्भुज के विकर्णों के वर्गों का योग भुजाओं के वर्गों के योग के बराबर होता है और इसके आधारों के गुणनफल का दोगुना होता है। एक समलम्ब चतुर्भुज के विकर्णों के इस गुण को एक पृथक प्रमेय के रूप में सिद्ध किया जा सकता है

2 ... यह सूत्र पिछले सूत्र को परिवर्तित करके प्राप्त किया जाता है। दूसरे विकर्ण के वर्ग को समान चिह्न से फेंका जाता है, जिसके बाद व्यंजक के बाएँ और दाएँ पक्षों से वर्गमूल निकाला जाता है।

3 ... एक समलम्बाकार विकर्ण की लंबाई ज्ञात करने का यह सूत्र पिछले एक के समान है, इस अंतर के साथ कि व्यंजक के बाईं ओर एक और विकर्ण छोड़ दिया गया है

सूत्रों का अगला समूह (4-5) अर्थ में समान है और समान अनुपात को व्यक्त करता है।

सूत्रों का समूह (6-7) आपको समलम्ब चतुर्भुज का विकर्ण ज्ञात करने की अनुमति देता है यदि समलंब का बड़ा आधार, एक भुजा और आधार पर कोण ज्ञात हो।

एक समलम्ब चतुर्भुज के विकर्णों को ऊँचाई के पदों में ज्ञात करने के सूत्र

ध्यान दें... यह पाठ समलम्ब चतुर्भुज के बारे में ज्यामिति की समस्याओं का समाधान प्रदान करता है। यदि आपको उस प्रकार की ज्यामिति समस्या का समाधान नहीं मिला है जिसमें आप रुचि रखते हैं - मंच पर एक प्रश्न पूछें.

टास्क.
समलम्ब चतुर्भुज ABCD (AD | | BC) के विकर्ण बिंदु O पर प्रतिच्छेद करते हैं। समलंब के आधार BC की लंबाई ज्ञात कीजिए यदि आधार AD = 24 सेमी, लंबाई AO = 9 सेमी, लंबाई OC = 6 सेमी है।

समाधान.
विचारधारा की दृष्टि से इस समस्या का समाधान बिल्कुल पिछली समस्याओं के समान है।

त्रिभुज AOD और BOC तीन कोणों में समान हैं - AOD और BOC लंबवत हैं, और अन्य कोण जोड़े में समान हैं, क्योंकि वे एक सीधी रेखा और दो समानांतर रेखाओं के प्रतिच्छेदन से बनते हैं।

चूँकि त्रिभुज समरूप होते हैं, उनके सभी ज्यामितीय आयाम एक दूसरे से संबंधित होते हैं, क्योंकि AO और OC खंडों के ज्यामितीय आयाम हमें समस्या कथन से ज्ञात होते हैं। अर्थात्

एओ / ओसी = एडी / बीसी
9/6 = 24 / ईसा पूर्व
ईसा पूर्व = 24 * 6/9 = 16

उत्तर: 16 सेमी

कार्य।
समलम्ब चतुर्भुज ABCD में, यह ज्ञात है कि AD = 24, BC = 8, AC = 13, BD = 5√17। समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।

समाधान ।
छोटे आधार B और C के शीर्षों से समलम्ब चतुर्भुज की ऊँचाई ज्ञात करने के लिए, हम दो ऊँचाइयों को बड़े आधार तक कम करते हैं। चूँकि समलम्ब चतुर्भुज असमान है, हम लंबाई AM = a, लंबाई KD = b ( सूत्र में संकेतन के साथ भ्रमित न होंट्रेपेज़ॉइड के क्षेत्र का पता लगाना)। चूँकि समलम्ब चतुर्भुज के आधार समानांतर हैं, और हमने बड़े आधार के लंबवत दो ऊँचाइयों को छोड़ दिया है, तो MBCK एक आयत है।

माध्यम
एडी = एएम + बीसी + केडी
ए + 8 + बी = 24
ए = 16 - बी

त्रिभुज DBM और ACK आयताकार हैं, इसलिए उनके समकोण समलम्ब चतुर्भुज की ऊँचाई से बनते हैं। आइए हम समलम्ब चतुर्भुज की ऊँचाई को h से निरूपित करें। फिर पाइथागोरस प्रमेय द्वारा

एच 2 + (24 - ए) 2 = (5√17) 2
तथा
एच 2 + (24 - बी) 2 = 13 2

हम ध्यान में रखते हैं कि a = 16 - b, फिर पहले समीकरण में
एच 2 + (24 - 16 + बी) 2 = 425
एच 2 = 425 - (8 + बी) 2

आइए पाइथागोरस प्रमेय द्वारा प्राप्त दूसरे समीकरण में ऊंचाई के वर्ग के मान को प्रतिस्थापित करें। हम पाते हैं:
425 - (8 + बी) 2 + (24 - बी) 2 = 169
- (64 + 16 बी + बी) 2 + (24 - बी) 2 = -256
-64 - 16 बी - बी 2 + 576 - 48 बी + बी 2 = -256
-64बी = -768
बी = 12

तो केडी = 12
कहा पे
एच 2 = 425 - (8 + बी) 2 = 425 - (8 + 12) 2 = 25
एच = 5

समलम्ब चतुर्भुज का क्षेत्रफल उसकी ऊँचाई और आधारों के योग के आधे से ज्ञात कीजिए
, जहाँ a b समलम्ब चतुर्भुज का आधार है, h समलम्ब चतुर्भुज की ऊँचाई है
एस = (24 + 8) * 5/2 = 80 सेमी 2

उत्तर: समलम्ब चतुर्भुज का क्षेत्रफल 80 सेमी 2 है।

- (ग्रीक ट्रेपेज़ियन)। 1) ज्यामिति में, एक चतुर्भुज जिसमें दो भुजाएँ समानांतर होती हैं, लेकिन दो नहीं। 2) जिम्नास्टिक अभ्यास के लिए अनुकूलित एक आकृति। रूसी भाषा में शामिल विदेशी शब्दों का शब्दकोश। चुडिनोव एएन, 1910. कीस्टोन ... ... रूसी भाषा के विदेशी शब्दों का शब्दकोश

चतुर्भुज- ट्रेपेज़ियम। कीस्टोन (ग्रीक ट्रेपेज़ियन से, शाब्दिक रूप से एक टेबल), एक उत्तल चतुर्भुज जिसमें दो पक्ष समानांतर होते हैं (ट्रेपेज़ॉइड के आधार)। समलम्ब चतुर्भुज का क्षेत्रफल आधारों (मध्य रेखा) और ऊँचाई के आधे योग के गुणनफल के बराबर होता है। ... सचित्र विश्वकोश शब्दकोश

चतुर्भुज, खोल, क्रॉसबार रूसी पर्यायवाची शब्दकोश। ट्रेपेज़ॉइड एन।, समानार्थक शब्द की संख्या: 3 क्रॉसबार (21) ... पर्यायवाची शब्दकोश

- (ग्रीक ट्रैपेज़ियन से, शाब्दिक रूप से एक टेबल), एक उत्तल चतुर्भुज जिसमें दो पक्ष समानांतर होते हैं (ट्रेपेज़ॉइड के आधार)। समलम्ब चतुर्भुज का क्षेत्रफल ऊँचाई के आधारों (मध्य रेखा) के आधे योग के गुणनफल के बराबर होता है ... आधुनिक विश्वकोश

- (ग्रीक से। ट्रैपेज़ियन शाब्दिक रूप से। तालिका), एक चतुर्भुज जिसमें दो विपरीत पक्ष, जिन्हें ट्रेपेज़ियम के आधार कहा जाता है, समानांतर हैं (आकृति एडी और बीसी में), और अन्य दो समानांतर नहीं हैं। आधारों के बीच की दूरी को समलम्ब चतुर्भुज की ऊँचाई कहा जाता है (पर ... ... बड़ा विश्वकोश शब्दकोश

कीस्टोन, एक चतुष्कोणीय सपाट आकृति जिसमें दो विपरीत भुजाएँ समानांतर होती हैं। समलम्ब चतुर्भुज का क्षेत्रफल समानांतर भुजाओं के आधे योग के बराबर होता है जो उनके बीच लंबवत की लंबाई से गुणा होता है ... वैज्ञानिक और तकनीकी विश्वकोश शब्दकोश

कीस्टोन, ट्रेपेज़, महिला (ग्रीक से। ट्रैपेज़ा टेबल)। 1. दो समानांतर और दो गैर-समानांतर पक्षों (चटाई) के साथ एक चतुर्भुज। 2. एक जिमनास्टिक उपकरण जिसमें दो रस्सियों (खेल) पर निलंबित क्रॉसबार होता है। एक्रोबेटिक ... ... उषाकोव का व्याख्यात्मक शब्दकोश

कीस्टोन, और, पत्नियां। 1. एक चतुर्भुज जिसकी दो समानांतर और दो गैर-समानांतर भुजाएँ हैं। ट्रेपेज़ॉइड के आधार (इसके समानांतर पक्ष)। 2. सर्कस या जिम्नास्टिक उपकरण, दो केबलों पर लटका हुआ क्रॉसबार। ओज़ेगोव का व्याख्यात्मक शब्दकोश। साथ … Ozhegov's Explanatory Dictionary

स्त्री, भू. असमान भुजाओं वाला एक चतुर्भुज, जिनमें से दो दीवार पर लगे (समानांतर) हैं। एक चतुर्भुज, एक चतुर्भुज की तरह, जिसमें सभी पक्ष अलग हो जाते हैं। ट्रेपेज़ोहेड्रोन, एक शरीर जो ट्रेपेज़ॉइड के साथ मुखरित होता है। डाहल का व्याख्यात्मक शब्दकोश। में और। डाहल। १८६३ १८६६... डाहल का व्याख्यात्मक शब्दकोश

- (ट्रेपेज़), यूएसए, 1956, 105 मिनट। मेलोड्रामा। महत्वाकांक्षी कलाबाज टीनो ओरसिनी सर्कस मंडली में प्रवेश करती है, जहां अतीत में एक प्रसिद्ध हवाई विज्ञानी माइक रिबल काम करता है। एक बार माइक ने टीनो के पिता के साथ परफॉर्म किया। युवा ओरसिनी माइक चाहता है ... ... सिनेमा का विश्वकोश

एक चतुर्भुज जिसमें दो भुजाएँ समानांतर होती हैं और दूसरी भुजाएँ समानांतर नहीं होती हैं। समानांतर भुजाओं के बीच की दूरी ऊंचाई टी। यदि समानांतर पक्षों और ऊंचाई में ए, बी और एच मीटर हैं, तो क्षेत्र टी में वर्ग मीटर है ... ब्रोकहॉस और एफ्रॉन का विश्वकोश