समारोह की समारोह और निरंतरता की सीमा का संचार। सीमा और निरंतरता

चर और निरंतर मूल्य

भौतिक मात्रा (समय, क्षेत्र, मात्रा, वजन, गति, आदि) को मापने के परिणामस्वरूप, उनके संख्यात्मक मान निर्धारित किए जाते हैं। गणित मूल्यों में लगी हुई है, जो उनकी विशिष्ट सामग्री से विचलित हो रही है। भविष्य में, मूल्यों की बात करते हुए, हम उनके संख्यात्मक मानों को ध्यान में रखेंगे। विभिन्न घटनाओं में, कुछ मूल्य बदलते हैं, जबकि अन्य अपने संख्यात्मक मूल्य को बनाए रखते हैं। उदाहरण के लिए, बिंदु, समय और दूरी परिवर्तन के समान आंदोलन के साथ, और गति स्थिर बनी हुई है।

परिवर्ती मूल्य मूल्य जो विभिन्न संख्यात्मक मान लेता है उसे कहा जाता है। जिस मान को संख्यात्मक मान नहीं बदलता है उसे कहा जाता है स्थायी। परिवर्तनीय मान पत्रों द्वारा दर्शाया जाएगा एक्स, वाई, जेड, ...स्थायी - ए, बी, सी, ...

ध्यान दें कि गणित में, निरंतर मूल्य को अक्सर एक विशेष परिवर्तनीय मामले के रूप में माना जाता है, जिसमें सभी संख्यात्मक मान समान होते हैं।

रजिस्ट्री क्षेत्र एक परिवर्तनीय मूल्य यह सभी संख्यात्मक मूल्यों का संयोजन है जो इसे बनाते हैं। परिवर्तन क्षेत्र में एक या कई अंतराल और एक बिंदु से हो सकते हैं।


क्रमबद्ध चर मूल्य। संख्या अनुक्रम

हम कहेंगे कि चर एक्स। यहां है क्रमबद्ध चर मूल्ययदि इसके परिवर्तन का क्षेत्र ज्ञात है, और किसी भी मूल्यों में से प्रत्येक के बारे में कहा जा सकता है कि उनमें से कौन पिछले एक है और बाद में क्या है।

एक आदेशित चर मूल्य का एक विशेष मामला किस रूप का एक चर मूल्य है संख्यात्मक अनुक्रम एक्स 1, एक्स 2, ..., एक्स एन, ... ऐसे मूल्यों के लिए जब मैं।< j, i, j Î N , मूल्य एक्स I. पूर्व निर्धारित, और एक्स जे। - इसके बाद, कोई फर्क नहीं पड़ता कि इनमें से कौन सा मूल्य अधिक है। इस प्रकार, संख्यात्मक अनुक्रम एक परिवर्तनीय मान है जिसका लगातार मूल्यों का नाम बदला जा सकता है। संख्यात्मक अनुक्रम को दर्शाया जाएगा। अनुक्रमों की अलग संख्या इसे बुलाया जाता है तत्वों.

उदाहरण के लिए, संख्यात्मक अनुक्रम निम्नलिखित मानों का निर्माण करता है:

समारोह

प्रकृति की विभिन्न घटनाओं का अध्ययन करते समय और तकनीकी समस्याओं को हल करने के लिए, और इसलिए, और गणित में आपको दूसरे में परिवर्तन के आधार पर एक मूल्य में परिवर्तन पर विचार करना होगा। तो, उदाहरण के लिए, यह ज्ञात है कि सर्कल का क्षेत्र सूत्र के त्रिज्या के माध्यम से व्यक्त किया जाता है S \u003d πR 2। अगर त्रिज्या आर विभिन्न संख्यात्मक मान लेता है, फिर क्षेत्र एस विभिन्न संख्यात्मक मान भी लेता है, यानी एक चर बदलने से दूसरे के परिवर्तन को शामिल किया जाता है।

यदि चर के प्रत्येक मूल्य एक्स।कुछ क्षेत्र से संबंधित किसी अन्य चर के एक निश्चित मूल्य से मेल खाता है वाईटी वाई बुला हुआ समारोह चर एक्स।। चलो प्रतीकात्मक रूप से लिखते हैं y \u003d f (x)। इस मामले में, चर एक्स। बुला हुआ स्वतंत्र चर या बहस.

अभिलेख y \u003d c।कहां है सी। - निरंतर, एक ऐसे कार्य को दर्शाता है जिसका मूल्य किसी भी मूल्य के लिए एक्स। वही और वही सी।.

कई मूल्य एक्स।जिसके लिए आप फ़ंक्शन के मानों को परिभाषित कर सकते हैं वाई नियम से f (x), बुला हुआ समारोह परिभाषा क्षेत्र.

ध्यान दें कि संख्यात्मक अनुक्रम भी एक समारोह है, जिसका परिभाषा क्षेत्र प्राकृतिक संख्याओं के सेट के साथ मेल खाता है।

मुख्य प्राथमिक कार्यों में गणित के स्कूल पाठ्यक्रम में अध्ययन किए गए सभी कार्यों शामिल हैं:

प्राथमिक समारोह इसे एक फ़ंक्शन कहा जाता है जिसे मुख्य प्राथमिक कार्यों द्वारा सेट किया जा सकता है और इसके अतिरिक्त, घटाव, गुणा, विभाजन और फ़ंक्शन से फ़ंक्शन लेने के संचालन की सीमित संख्या के साथ स्थिर किया जा सकता है।

संख्यात्मक अनुक्रम की सीमा की अवधारणा

गणित के एक और वर्ष में, सीमा की अवधारणा मौलिक भूमिका निभाएगी, क्योंकि यह सीधे गणितीय विश्लेषण की मूल अवधारणाओं से संबंधित है - एक व्युत्पन्न, अभिन्न, आदि।

आइए संख्यात्मक अनुक्रम की सीमा की अवधारणा से शुरू करें।

संख्या ए। बुला हुआ सीमा दृश्यों एक्स। = {एक्स एन) यदि मनमानी पूर्वनिर्धारित मनमानी निर्दिष्ट संख्या के लिए ऐसी प्राकृतिक संख्या है एनउस पर n\u003e एन। असमानता | एक्स एन - ए |< ε.

अगर संख्या ए। एक अनुक्रम सीमा है एक्स। = {एक्स एन), तो वे कहते हैं कि एक्स एन करना चाहता है ए।, और लिखा।

ज्यामितीय शर्तों में इस परिभाषा को तैयार करने के लिए, हम निम्नलिखित अवधारणा पेश करते हैं।

पड़ोस प्वाइंट एक्स 0 एक मनमाना अंतराल कहा जाता है ( ए, बी।), इस बिंदु को अपने अंदर रखें। अक्सर बिंदु के पड़ोस को मानता है x 0, जिसके लिए x 0 मध्य है, फिर x 0 बुला हुआ केन्द्र पड़ोस, और मूल्य ( बी–ए।)/2 – rADIUS अड़ोस - पड़ोस।

इसलिए, हम पता लगाते हैं कि संख्यात्मक अनुक्रम की सीमा की ज्यामितीय रूप से अवधारणा का क्या अर्थ है। ऐसा करने के लिए, हम फॉर्म में परिभाषा से नवीनतम असमानता लिखते हैं

इस असमानता का अर्थ है कि संख्याओं के साथ सभी अनुक्रम तत्व n\u003e एन। अंतराल में झूठ होना चाहिए (a - ε; a + ε)।

नतीजतन, एक निरंतर संख्या ए। संख्यात्मक अनुक्रम की एक सीमा है ( एक्स एन) यदि इस बिंदु पर केंद्र के साथ किसी भी छोटे पड़ोस के लिए ए। त्रिज्या ε (ε - प्वाइंट पड़ोस ए।) संख्या के साथ एक अनुक्रम तत्व है एनसभी बाद के तत्व संख्या n\u003e एन। इस पड़ोस के अंदर होगा।

उदाहरण।

हम कई टिप्पणियां करेंगे।

नोट 1। जाहिर है, यदि संख्यात्मक अनुक्रम के सभी तत्व समान निरंतर मान लेते हैं x n \u003d cइस अनुक्रम की सीमा सबसे निरंतर के बराबर होगी। दरअसल, किसी भी ε हमेशा असमानता करता है | एक्स एन - सी| = |सी - सी।| \u003d 0 & lt ε।

नोट 2। सीमा निर्धारण से यह इस प्रकार है कि अनुक्रम में दो सीमाएं नहीं हो सकती हैं। वास्तव में ऐसा मानते हैं x n → a और उस समय पर ही एक्स एन → बी। किसी को भी लें और अंक के परिवेश पर ध्यान दें। ए। तथा बी त्रिज्या ε (चित्र देखें)। फिर परिभाषा सीमा से, अनुक्रम के सभी तत्व, कुछ से शुरू होने के कारण, बिंदु के पड़ोस में होना चाहिए लेकिन अऔर बिंदु के पड़ोस में बीवह असंभव है।

नोट 3। ऐसा मत सोचो कि प्रत्येक संख्यात्मक अनुक्रम की सीमा है। उदाहरण के लिए, एक परिवर्तनीय मान मान लेता है। । यह देखना आसान है कि यह अनुक्रम किसी भी सीमा की तलाश नहीं करता है।

समारोह सीमा

समारोह y \u003d f (x) बिंदु के कुछ पड़ोस में निर्धारित ए।। मान लीजिए एक स्वतंत्र चर एक्स। असीमित आ रहा है ए।। इसका मतलब है कि हम दे सकते हैं एच कुछ के करीब ए।लेकिन बराबर नहीं ए।। हम इसे अस्वीकार कर देंगे एक्स → ए।। उन लोगों के लिए एक्स। फ़ंक्शन के उचित मान पाएं। यह हो सकता है कि मूल्य f (x) कुछ संख्या के लिए असीमित दृष्टिकोण भी बी.Then कहते हैं कि संख्या बी एक सीमा समारोह है f (x)के लिये एक्स → ए।.

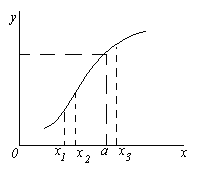
हम समारोह की सीमा का सख्त निर्धारण शुरू करते हैं।

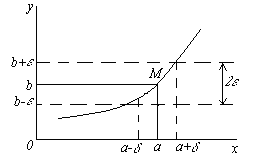
समारोह y \u003d f (x) x → at पर b को सीमित करता हैयदि प्रत्येक सकारात्मक संख्या ε के लिए, इससे कोई फर्क नहीं पड़ता कि यह कितना छोटा था, इस तरह के सकारात्मक संख्या को निर्दिष्ट करना संभव है δ जो कि सभी x ≠ ए पर असमानता को संतुष्ट करने के क्षेत्र से निर्धारित करने के क्षेत्र से | एक्स - ए।| < δ, имеет место неравенство |f (x) - बी| < ε. Если बी एक सीमा समारोह है f (x) के लिये एक्स → ए।, फिर लिखें या f (x) → b के लिये एक्स → ए।.

हम फ़ंक्शन ग्राफ़ पर इस परिभाषा को चित्रित करते हैं। चूंकि असमानता से | एक्स - ए।| < δ должно следовать неравенство |f (x) - बी| < ε, т.е. при एक्स। Î ( ए। - δ, ए। + δ) संबंधित कार्यों f (x) Î ( बी - ε, बी + ε), फिर, मनमाने ढंग से ε\u003e 0 लेना, हम इस तरह के एक नंबर को उठा सकते हैं δ कि सभी बिंदुओं के लिए एक्स।δ में झूठ बोलना - बिंदु का पड़ोस ए।समारोह के कार्य के कार्य के अनुरूप स्ट्रिप 2ε चौड़े, सीमित प्रत्यक्ष के अंदर झूठ होना चाहिए y \u003d B. - I. I. y \u003d B. + ε.

यह ध्यान रखना आसान है कि फ़ंक्शन की सीमा में संख्यात्मक अनुक्रम की सीमा के समान गुण होना चाहिए, अर्थात्, यदि एक्स → ए। फ़ंक्शन की एक सीमा है, फिर यह एकमात्र है।

उदाहरण।

एक असीमित रिमोट पॉइंट में समारोह की सीमा की अवधारणा

अब तक, हमने वैरिएबल होने पर मामले की सीमाओं को माना है एक्स। यह एक निश्चित निरंतर संख्या की मांग की।

हम कहेंगे कि चर x इन्फिनिटी में जाता हैयदि प्रत्येक पूर्व निर्धारित सकारात्मक संख्या के लिए म। (यह उतना पुराना हो सकता है) निर्दिष्ट किया जा सकता है x \u003d x 0जिससे वेरिएबल के सभी बाद के मूल्य असमानता को पूरा करेंगे | एक्स |\u003e एम.

उदाहरण के लिए, चर को दें एच मान लेता है एक्स। 1 = –1, एक्स। 2 = 2, एक्स। 3 = –3..., एक्स n \u003d (- 1) एन एन, ... यह स्पष्ट है कि यह एक असीम रूप से बड़ा चर मूल्य है, क्योंकि बिल्कुल भी म। \u003e 0 वैरिएबल के सभी मान, कुछ के साथ शुरू, पूर्ण मूल्य में और अधिक होगा म।.

परिवर्ती मूल्य x → + ∞अगर मनमानी पर म। \u003e 0 चर के सभी बाद के मूल्य, कुछ से शुरू, असमानता को संतुष्ट करते हैं एक्स\u003e एम।.

इसी तरह, एक्स। → - ∞, अगर किसी पर म। > 0 एक्स।< -M .

हम कहेंगे कि समारोह f (x) वह सीमा के लिए प्रयास करता है बी के लिये एक्स। → ∞, यदि मनमानी छोटे सकारात्मक संख्या ε के लिए इस तरह के सकारात्मक संख्या को निर्दिष्ट किया जा सकता है म।सभी मूल्यों के लिए एक्स।संतोषजनक असमानता | एक्स |\u003e एम, असमानता प्रदर्शन किया जाता है f (x) - बी| < ε.

निरूपित।

उदाहरण।

असीम रूप से बड़ी विशेषताएं

पहले, हमने मामलों को माना जाता है f (x) कुछ अंत सीमा की मांग की बी के लिये एक्स → ए। या एक्स। → ∞.

फ़ंक्शन होने पर अब इस मामले पर विचार करें y \u003d f (x) तर्क बदलने की कुछ विधि।

समारोह f (x) जब अनंतता होती है एक्स → ए।। है एक असीम रूप में बड़ा मान यदि किसी भी संख्या के लिए म।इससे कोई फर्क नहीं पड़ता कि यह कितना बड़ा हो सकता है, आप ऐसे δ\u003e 0 पा सकते हैं, जो सभी मूल्यों के लिए एच≠ए।संतोषजनक स्थिति | एक्स-ए।| < δ, имеет место неравенство |f (x)| > म।.

यदि एक f (x) जब अनंतता होती है एक्स → ए।, फिर लिखें या f (x)→ ∞ एक्स → ए।.

जब मामले के लिए एक समान परिभाषा निर्दिष्ट करें एक्स।→∞.

यदि एक f (x) जब अनंतता होती है एक्स → ए। और साथ ही साथ क्रमशः केवल सकारात्मक या केवल नकारात्मक मान लेता है, लिखता है या।

उदाहरण।

सीमित कार्य

एक फ़ंक्शन को निर्दिष्ट करने दें y \u003d f (x)कुछ सेट पर परिभाषित डी तर्क के मूल्य।

समारोह y \u003d f (x) बुला हुआ सीमित मंच पर डीयदि कोई सकारात्मक संख्या है म। जैसे कि सभी मूल्यों के लिए एक्स। माना गया सेट से, असमानता का प्रदर्शन किया जाता है | एफ (एक्स) | ≤M। अगर ऐसा नंबर म। कोई समारोह नहीं है f (x) बुला हुआ असीमित मंच पर डी.

उदाहरण।

  1. समारोह वाई\u003d पाप एक्स।-∞ में परिभाषित<एक्स।<+∞, является ограниченной, так как при всех значениях एक्स। | पाप एक्स।|≤1 = म।.
  2. समारोह वाई\u003d x 2 +2 सीमित है, उदाहरण के लिए, एक सेगमेंट पर, क्योंकि बिल्कुल भी एक्स। इस कट से | एफ (एक्स) | ≤f।(3) = 11.
  3. एक समारोह पर विचार करें वाई\u003d ln। एक्स। के लिये एक्स। Î (0; 1)। यह फ़ंक्शन निर्दिष्ट खंड पर असीमित है, क्योंकि एक्स।→ 0 ln। एक्स।→-∞.

समारोह y \u003d f (x) बुला हुआ एक्स → ए पर सीमितयदि इस बिंदु पर केंद्र के साथ एक पड़ोस है लेकिन अजिसमें समारोह सीमित है।

समारोह y \u003d f (x) बुला हुआ एक्स → ∞ पर सीमितअगर ऐसा नंबर है N\u003e0 कि सभी मूल्यों पर एच | एक्स |\u003e एनसमारोह f (x) सीमित।

हम सीमित फ़ंक्शन और एक फ़ंक्शन के बीच एक लिंक स्थापित करते हैं।

प्रमेय 1। अगर बी - परिमित संख्या, फिर समारोह f (x) तक सीमित एक्स → ए।.

सबूत। चूंकि , किसी भी ε\u003e 0 के साथ ऐसा नंबर δ\u003e 0 है, जो सभी मूल्यों पर है एचसंतोषजनक असमानता | एक्स-ए |< Δ, असमानता का प्रदर्शन किया जाता है | एफ (एक्स) -बी |< ε। मॉड्यूल की संपत्ति का उपयोग करना | एफ (एक्स) - बी | ≥ | एफ (एक्स) | - | बी |, मैं फॉर्म में अंतिम असमानता लिखूंगा | एफ (एक्स) |<|b|+ ε। इस प्रकार, यदि आप डालते हैं एम \u003d | बी | + ε, तब कब एक्स → ए | एफ (एक्स) |

टिप्पणी। सीमित समारोह की परिभाषा से यह इस प्रकार है कि अगर, यह असीमित है। हालांकि, विपरीत गलत है: एक असीमित फ़ंक्शन असीमित रूप से बड़ा नहीं हो सकता है। एक उदाहरण दें।

प्रमेय 2। यदि, तो समारोह y \u003d 1 / f (x) तक सीमित एक्स → ए।.

सबूत। प्रमेय की स्थिति से यह बिंदु के कुछ पड़ोस में एक मनमाने ढंग से ε\u003e 0 के साथ आता है ए। है | एफ (एक्स) - बी |< ε। चूंकि | एफ (एक्स) - बी | \u003d | बी - एफ (एक्स) | ≥ | बी | - | एफ (एक्स) |टी | बी | - | एफ (एक्स) |< ε। इसलिये, | एफ (एक्स) |\u003e | बी | -ε\u003e 0। इसीलिए

जेड (0, ± 1, ± 2, ± 3, ...) कई पूर्णांक संख्या। पूर्णांक की संख्या में कई प्राकृतिक शामिल हैं। प्र विभिन्न प्रकार की तर्कसंगत संख्या। पूरी संख्या भी भिन्न हैं। अंश फॉर्म की अभिव्यक्ति है, जहां पी एक पूर्णांक है, क्यू एक प्राकृतिक है। फॉर्म में दशमलव अंश भी लिखा जा सकता है। उदाहरण के लिए: 0.25 \u003d 25/100 \u003d 1/4। पूर्णांक भी रूप में लिखा जा सकता है। उदाहरण के लिए, एक denominator के साथ एक अंश के रूप में "एक": 2 \u003d 2 / 1. क्रम में, किसी भी तर्कसंगत संख्या को दशमलव अंश के साथ रिकॉर्ड किया जा सकता है - निश्चित रूप से या अनंत आवधिक। आर सभी वास्तविक संख्याओं में से कई। अपरिमेय संख्या अनंत गैर-आवधिक अंश हैं। इनमें शामिल हैं: एक साथ दो सेट (तर्कसंगत और तर्कहीन संख्याएं) - कई मान्य (या वास्तविक) संख्याएं बनाएं।

यदि सेट में एक तत्व नहीं होता है, तो इसे कहा जाता है खाली सेट और रिकॉर्ड किया गया Ø .

सीमांत अस्तित्व

∃- सीमांत अस्तित्व, "मौजूद" शब्दों के बजाय उपयोग किया जाता है,

"उपलब्ध।" वर्णों का संयोजन ∃!, जो पढ़ा जाता है केवल एक ही है।

निरपेक्ष मूल्य

परिभाषा। वास्तविक संख्या के पूर्ण मूल्य (मॉड्यूल) को गैर-ऋणात्मक संख्या कहा जाता है, जो सूत्र द्वारा निर्धारित किया जाता है:

उदाहरण के लिए,

मॉड्यूल की गुण

यदि दोनों वैध संख्याएं हैं, तो समानता सत्य है:

समारोह

दो या दो से अधिक मानों के बीच संबंध जिसमें फ़ंक्शन के तर्कों को नामित करने वाले कुछ मानों के प्रत्येक मान को फ़ंक्शन के मानों को नामक अन्य मानों के मानों के अनुरूप रखा जाता है ।

समारोह परिभाषा क्षेत्र

फ़ंक्शन परिभाषा फ़ील्ड को एक स्वतंत्र परिवर्तनीय एक्स के मान कहा जाता है, जिसमें फ़ंक्शन में शामिल सभी ऑपरेशन किए जाएंगे।

निरंतर कार्य

फंक्शन एफ (एक्स), बिंदु ए के कुछ पड़ोस में परिभाषित, को इस बिंदु पर निरंतर कहा जाता है अगर

संख्यात्मक अनुक्रम

प्रकार का कार्य वाई= एफ(एक्स।), एक्स।के बारे में एन,कहा पे एन- प्राकृतिक संख्याओं का सेट (या प्राकृतिक तर्क का कार्य) इंगित किया गया है वाई= एफ(एन) या वाई 1 , वाई 2 ,…, y N।.... मूल्यों वाई 1 , वाई 2 , वाई 3, ... तदनुसार पहले, दूसरा, तीसरा, ... अनुक्रम सदस्य।

निरंतर तर्क के कार्य की सीमा

संख्या ए को x-\u003e x0 पर फ़ंक्शन y \u003d f (x) की सीमा कहा जाता है, यदि सभी मान x के लिए, संख्या x0 से थोड़ा अलग है, फ़ंक्शन f (x) के संबंधित मान के रूप में जैसा कि यह संख्या ए से अलग है

असीम रूप से छोटी सुविधा

समारोह y \u003d f (x) बुला हुआ असीम रूप से छोटा के लिये एक्स → ए। या के लिए एक्स।→ ∞, अगर या, यानी। असीम रूप से छोटा कार्य एक समारोह है जिसकी सीमा इस बिंदु पर शून्य है।

सीमा और निरंतरता

एक चर के कार्य

3.1.1। परिभाषा। संख्या लेकिन अ एक्स। लग रहा है। एक्स। 0, यदि किसी भी संख्या के लिए
एक संख्या है
(
), और स्थिति पूरी हो जाएगी:

यदि एक
टी
.

(प्रतीकवाद:
).

यदि अनुसूची का बिंदु जी कार्यों

कब अ असीमित निकटता के दृष्टिकोण (उनको।
), (चित्र 3.1 देखें), यह परिस्थिति किस समारोह के एक ज्यामितीय समतुल्य है
के लिये
सीमा मान (सीमा) है ए। (प्रतीकवाद:
).

समारोह अनुसूची,

अंजीर। 3.1।

यह ध्यान दिया जाना चाहिए कि जब फ़ंक्शन के सीमा मान (सीमा) को निर्धारित करने में एक्स। की तलाश कर रहा है। एक्स। 0 बिंदु पर कार्य के व्यवहार के बारे में कुछ भी नहीं कहता है एक्स। 0। बहुत बिंदु पर एक्स। 0 फ़ंक्शन निर्धारित नहीं किया जा सकता है, शायद
, हो सकता है
.

यदि एक
, फ़ंक्शन को असीम रूप से छोटा कहा जाता है
.

गैप कहा जाता है - पड़ोस का बिंदु एक्स। एक क्रैक सेंटर के साथ 0। इस नाम का उपयोग करके, यह इस तरह कहा जा सकता है: यदि किसी भी संख्या के लिए कोई संख्या है, और स्थिति का प्रदर्शन किया जाएगा: यदि
टी
.

3.1.2। परिभाषा। यदि किसी भी अभिसरण के लिए एक्स। 0 अनुक्रम
अनुक्रम
क। लेकिन अ.

3.1.3। हम विभाजन परिभाषाओं 3.1.1 और 3.1.2 के बराबर साबित करते हैं

पहली परिभाषा के अर्थ में पहले और चलो
(
), तो सब उनके अंतिम संख्या को संतुष्टता के अलावा
कहां है द्वारा चुना गया पहली परिभाषा के अर्थ में, यानी
। पहली परिभाषा से निम्नानुसार है। चलो
दूसरी परिभाषा के अर्थ में और मान लें कि दूसरी परिभाषा के अर्थ में
। कुछ के लिए एक मनमाने ढंग से छोटे (उदाहरण के लिए, जब
) एक अनुक्रम मिला
लेकिन उसी समय पर
। विरोधाभास के लिए आया, इसलिए, दूसरी परिभाषा से यह इस प्रकार है।

3.1.4। इन परिभाषाओं की समतुल्यता विशेष रूप से सुविधाजनक है, अनुक्रमों के लिए सीमाओं के गुणों पर सभी सबसे सिद्ध प्रमेय के लिए लगभग एक नए मामले में स्वचालित रूप से स्थानांतरित की जाती है। सीमाओं की अवधारणा को स्पष्ट करने के लिए केवल आवश्यक है। इसी प्रमेय के पास निम्नलिखित शब्द है:

यदि एक
, फिर कुछ  तक सीमित - बिंदु के पड़ोस एक्स। एक क्रैक सेंटर के साथ 0।

3.2.1 .torem। रहने दो
,
,

तब फिर,
,

,

.

3.2.2। रहने दो

- मनमाना, कनवर्ट करना एक्स। 0 कार्यों के तर्कों के मूल्यों का क्रम और
। प्रासंगिक अनुक्रम
तथा
इन कार्यों के मूल्यों में सीमाएं हैं ए। तथा बी। लेकिन फिर, विभाजन प्रमेय 2.13.2, अनुक्रम के आधार पर
,
तथा
क्रमशः, समान सीमाएं हैं ए। +बी,
तथा
। बिंदु पर समारोह की सीमा की परिभाषा के अनुसार (धारा 2.5.2 देखें), इसका मतलब है कि

,
,

.

3.2.3। प्रमेय। यदि एक
,
और कुछ परिवेश में

तब होता है


.

3.2.4। बिंदु पर समारोह की सीमा को परिभाषित करके एक्स। 0 किसी भी अनुक्रम के लिए
ऐसा है कि

फ़ंक्शन मानों का कार्य एक सीमा बराबर है लेकिन अ। इसका मतलब है कि किसी के लिए
एक संख्या है
प्रदर्शन किया । इसी तरह, अनुक्रम के लिए
एक संख्या है
ऐसा कि किसी भी कमरे के लिए
प्रदर्शन किया । का चयन
हम सभी के लिए मिलता है
प्रदर्शन किया । असमानताओं की इस श्रृंखला से हमारे पास किसी के लिए है, जिसका अर्थ है कि
.

3.2.5। परिभाषा। संख्या लेकिन अ जब सीमा मान (सीमा) फ़ंक्शन कहा जाता है एक्स। लग रहा है। एक्स। 0 सही (प्रतीकवाद:
)यदि कोई संख्या एक संख्या है () और स्थिति निष्पादित की जाएगी: यदि
टी
.

कई को सही  - बिंदु का पड़ोस कहा जाता है एक्स। 0। इसी प्रकार, बाईं ओर सीमा मान (सीमा) की अवधारणा (
).

3.2.6। प्रमेय। फ़ंक्शन जब एक सीमा मान (सीमा) समान है लेकिन अ तब और केवल कब

,

3.3.1। परिभाषा। संख्या लेकिन अ जब सीमा मान (सीमा) फ़ंक्शन कहा जाता है एक्स। अनंत की तलाश अगर किसी भी संख्या के लिए कोई संख्या है
(
) और स्थिति पूरी हो जाएगी:

यदि एक
तब फिर।

(प्रतीकवाद:
.)

बहुत से
बुला हुआ डी-स्टेस्ट अनंतता।

3.3.2। परिभाषा। संख्या लेकिन अ जब सीमा मान (सीमा) फ़ंक्शन कहा जाता है एक्स। यदि किसी भी संख्या के लिए कोई संख्या है तो प्लस अनंत की तलाश में डी () शर्तों को पूरा किया जाएगा:

यदि एक
तब फिर।

(प्रतीकवाद:
).

यदि अनुसूची का बिंदु जी कार्यों
असीमित वृद्धि के साथ
असीमित एकमात्र क्षैतिज प्रत्यक्ष
(चित्र 3.2 देखें), तो यह परिस्थिति किस समारोह के एक ज्यामितीय समतुल्य है
के लिये
संख्या के बराबर एक सीमा मान (सीमा) है ए। (प्रतीकवाद:
).

अनुसूची समारोह
,

बहुत से
बुला हुआ डी-कस्ट प्लस अनंतता।

इसी तरह, सीमा की अवधारणा निर्धारित की जाती है
.

व्यायाम।

निम्नलिखित मामलों के संबंध में सीमाओं के बारे में सभी प्रमेय शब्द:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1। परिभाषा। फ़ंक्शन को असीमित बड़े फ़ंक्शन (या बस असीम रूप से बड़ा) कहा जाता है, जब किसी भी संख्या के लिए

संतोषजनक असमानता को असमानता की जाती है
.

(प्रतीकवाद:
.)

अगर चल रहा है
, फिर लिखना
.

अगर चल रहा है
, फिर लिखना
.

3.4.2। प्रमेय। रहने दो
तथा
के लिये
.

फिर
- असीम रूप से एक बड़ा कार्य।

3.4.3। एक मनमानी संख्या दें। चूंकि यह एक असीम रूप से छोटा कार्य है, फिर संख्या के लिए
एक संख्या है जो सभी के लिए एक्स। इस तरह की असमानता की जाती है
लेकिन फिर उसी के लिए एक्स। असमानता की जाती है
। वे। - असीम रूप से एक बड़ा कार्य।

3.4.4 .torem। जब और पर असीम रूप से एक बड़ा कार्य हो।

फिर - असीम रूप से छोटे कार्य पर।

(यह प्रमेय विभाजन खंड 3.8.2 के समान साबित हुआ है)।

3.4.5। समारोह
जब असीमित कहा जाता है
यदि किसी भी संख्या के लिए
और किसी भी δ-नेबरहुड प्वाइंट आप एक बिंदु निर्दिष्ट कर सकते हैं एक्स। इस पड़ोस से ऐसा
.

3.5.1। परिभाषा। फ़ंक्शन कहा जाता है निरंतर बिंदु पर , यदि एक
.

अंतिम स्थिति दर्ज की जा सकती है और इसी तरह:

.

इस रिकॉर्ड का अर्थ है कि निरंतर कार्यों के लिए सीमा चिह्न और फ़ंक्शन चिह्न बदला जा सकता है।

या ऐसा:। या फिर, शुरुआत में।

निरूपित
। फिर
और \u003d।
और रिकॉर्डिंग का अंतिम रूप एक दृश्य ले जाएगा

.

संकेत के तहत अभिव्यक्ति एक सीमा है जो वेतन वृद्धि के कारण एक बिंदु के कार्य की वृद्धि है
बहस एक्स। बिंदु पर, नामित आमतौर पर पसंद है
। नतीजतन, हम बिंदु पर रिकॉर्डिंग की स्थिति निरंतरता की स्थिति का निम्नलिखित रूप प्राप्त करते हैं

,

जिसे बिंदु पर समारोह की निरंतरता की "कार्य परिभाषा" कहा जाता है।

फ़ंक्शन कहा जाता है निरंतर बिंदु पर बाएं, यदि एक
.

फ़ंक्शन कहा जाता है निरंतर बिंदु पर दाहिने तरफ, यदि एक
.

3.5.2। उदाहरण।
। यह सुविधा किसी के लिए निरंतर है। सीमा गुण प्रमेय का उपयोग करके, हम तुरंत प्राप्त करते हैं: कोई भी तर्कसंगत कार्य प्रत्येक बिंदु पर निरंतर होता है जिसमें इसे परिभाषित किया जाता है, यानी प्रकार का कार्य
.

अभ्यास.

3.6.1। स्कूल की पाठ्यपुस्तक में (उच्च स्तर की कठोरता पर) साबित होता है
(पहली अद्भुत सीमा)। दृश्य ज्यामितीय विचारों से यह तुरंत बाहर निकलता है
। ध्यान दें कि बाएं असमानता से यह भी इसुपाद होता है
। वह समारोह
शून्य में निरंतर। यहां से सभी बिंदुओं पर सभी त्रिकोणमितीय कार्यों की निरंतरता को साबित करना बिल्कुल मुश्किल है जहां उन्हें परिभाषित किया गया है। वास्तव में, कब
असीम रूप से छोटे कार्यों का काम कैसा है
सीमित समारोह पर
.

3.6.2। (दूसरी अद्भुत सीमा)। हम पहले से ही कैसे जानते हैं

,

कहा पे प्राकृतिक संख्या चलती है। आप यह दिखा सकते हैं
। अतिरिक्त
.

अभ्यास.


3.7.1। प्रमेय (एक जटिल समारोह की निरंतरता के बारे में)।

अगर समारोह
बिंदु पर निरंतर और
, और समारोह
निरंतर बिंदु , फिर एक जटिल कार्य
निरंतर बिंदु।

3.7.2। इस अनुमोदन की वैधता तुरंत प्रपत्र में दर्ज निरंतरता की परिभाषा से होती है:

3.8.1। प्रमेय। समारोह प्रत्येक बिंदु पर निरंतर (
).

3.8.2। यदि आप उचित मानते हैं, तो समारोह
किसी के लिए परिभाषित किया गया है और सख्ती से एक नीरस है (सख्ती से घट रहा है
सख्ती से बढ़ रहा है
), प्रमाण मुश्किल नहीं है।

के लिये
हमारे पास है:

वे। कब मिलेगा
क्या मतलब है कि समारोह के साथ निरंतर।

के लिये
सब कुछ पिछले एक के लिए आता है:

के लिये
.

के लिये
समारोह
लगातार, लगातार लगातार।

3.9.1। प्रमेय (फ़ीड फ़ंक्शन की सह-अस्तित्व और निरंतरता के बारे में)।

एक निरंतर कार्य को सख्ती से कमी (सख्ती से बढ़ता है) कुछ δ में - बिंदु के पड़ोस,
। फिर कुछ ε में - बिंदु का पड़ोस एक रिवर्स फ़ंक्शन है
जो सख्ती से घटता है (सख्ती से बढ़ता है) और बिंदु के पड़ोस में ε में निरंतर है।

3.9.2। हम यहां बिंदु पर रिवर्स फ़ंक्शन की निरंतरता को साबित करते हैं।

बात करना वाई बिंदुओं के बीच स्थित है
तथा
इसलिए अगर
टी
कहां है।

3.10.1। तो, निरंतर कार्यों पर कोई भी अनुमोदित अंकगणितीय क्रियाएं फिर से निरंतर कार्यों का कारण बनती हैं। जटिल और व्यस्त कार्यों का गठन निरंतरता खराब नहीं करता है। इसलिए, कुछ और जिम्मेदारी के साथ, हम तर्क दे सकते हैं कि तर्क के सभी अनुमोदित मूल्यों के साथ सभी प्राथमिक कार्य निरंतर हैं।

व्यायाम.

साबित करो
के लिये
(दूसरी उल्लेखनीय सीमा का एक और रूप)।

3.11.1। असीमित रूप से छोटे की अवधारणा द्वारा उपयोग की जाने वाली सीमा गणना बहुत सरल है। साम्राज्य कार्यों के मामले में संक्षेप में समकक्ष की अवधारणा सुविधाजनक है।

परिभाषा। कार्य और जब समतुल्य कहा जाता है
(बजाय तुम लिख सकते हो
,
,
,
,
).

प्रयुक्त पदनाम एफ ~ जी.

समतुल्यता में निम्नलिखित गुण हैं

असीमित रूप से छोटे समकक्ष की निम्नलिखित सूची को याद रखना आवश्यक है:

~
के लिये
; (1)

~ कब अ; (2)

~
कब अ; (3)

~ कब अ; (चार)

~ कब अ; (पांच)

~ कब अ; (6)

~ कब अ; (7)

~ पी कब अ; (आठ)

~ के लिये
; (9)

~
पर। (10)

यहां और स्वतंत्र चर नहीं हो सकता है, लेकिन कार्य
तथा
कुछ व्यवहार के साथ शून्य और इकाई के क्रमशः मांगना एक्स।। उदाहरण के लिए,

~
 के लिये
,

~
के लिये
.

समतुल्यता (1) पहली उल्लेखनीय सीमा की रिकॉर्डिंग का एक अलग रूप है। समानता (2), (3), (6) और (7) सीधे साबित किया जा सकता है। समतुल्यता (4) (1) से प्राप्त होती है (1) गुणों को ध्यान में रखते हुए 2) समकक्ष:

~
.

इसी तरह (5) और (7) (2) और (6) से प्राप्त होते हैं। वास्तव में

~
,

~
.

समकक्ष (8) अनुक्रमिक उपयोग (7) और (6) द्वारा साबित होता है:

a (9) और (10) (6) और (8) प्रतिस्थापन से प्राप्त होते हैं
.

3.11.2। प्रमेय। काम और रिश्ते में सीमा की गणना करते समय, आप कार्यों को समकक्ष में बदल सकते हैं। अर्थात्, अगर ~
, फिर, या दोनों सीमाएं एक ही समय में मौजूद नहीं हैं, और
या इनमें से दोनों सीमाएं एक ही समय में मौजूद नहीं हैं।

हम पहली समानता साबित करते हैं। एक सीमा को कहें, कहो,
मौजूद। फिर

.

3.11.3। चलो (- एक संख्या या प्रतीक,
या
)। हम विभिन्न बीएम के व्यवहार पर विचार करेंगे। कार्य (इसलिए हम शब्द को असीम रूप से छोटा कर देंगे)।

परिभाषाएँ।
और समतुल्य बीएम कहा जाता है। कार्य कब
(कब अ)।

हम बीएम को फोन करेंगे। बीएम की तुलना में उच्च क्रम समारोह
, यदि एक
(कब अ)।

3.11.4। यदि बीएम के बराबर है। कार्य, टी।
बीएम हैं। से अधिक क्रम समारोह
और क्या। - बीएम जिनके साथ सभी एक्स के लिए कार्य करता है और, यदि इस बिंदु पर फ़ंक्शन को डिस्पोजेबल ब्रेक पॉइंट कहा जाता है। यह दूसरी तरह का अंतर है। खुद को इंगित करें परीक्षा

Colloquium के लिए। अनुभाग: " सीमा तथा निरंतरताकार्यों वैध वैरिएबल " कार्योंएकवैरिएबल ""अंतर कलन कार्यों कई चर "

  • नियंत्रण कार्यों और प्रश्नों के विषय और उदाहरण (परीक्षण कार्य करता है व्यक्तिगत मानक गणना बोलोक्वियम) मैं सेमेस्टर परीक्षा №1 अनुभाग "वैध चर के कार्य की सीमा और निरंतरता"

    परीक्षा

    Colloquium के लिए। अनुभाग: " सीमा तथा निरंतरताकार्यों वैध वैरिएबल ""अंतर कलन कार्योंएकवैरिएबल ""अंतर कलन कार्यों कई चर "। संख्यात्मक अनुक्रम ...

  • परीक्षा

    Colloquium के लिए। अनुभाग: " सीमा तथा निरंतरताकार्यों वैध वैरिएबल ""अंतर कलन कार्योंएकवैरिएबल ""अंतर कलन कार्यों कई चर "। संख्यात्मक अनुक्रम ...

  • विषयों और नियंत्रण कार्यों और प्रश्नों के उदाहरण (परीक्षण कार्य व्यक्तिगत मानक गणना बोलोक्वियम) मैं सेमेस्टर परीक्षण कार्य अनुभाग "सीमा और वास्तविक चर के कार्य की निरंतरता"

    परीक्षा

    Colloquium के लिए। अनुभाग: " सीमा तथा निरंतरताकार्यों वैध वैरिएबल ""अंतर कलन कार्योंएकवैरिएबल ""अंतर कलन कार्यों कई चर "। संख्यात्मक अनुक्रम ...

  • व्याख्यान 19 की सीमा और कई चर के समारोह की निरंतरता

    भाषण

    ... सीमा तथा निरंतरताकार्यों कई चर। 19.1। संकल्पना कार्यों कई चर। संशोधन करके कार्यों कई चर ... गुण कार्योंएकपरिवर्तनशील, निरंतर खंड पर। गुण देखें कार्यों, निरंतर पर...

    • संख्यात्मक अनुक्रम की सीमा की अवधारणा

    संख्यात्मक अनुक्रम को निर्धारित करने वाले पहले को याद करना।

    परिभाषा 1।

    वैध संख्याओं के एक सेट पर कई प्राकृतिक संख्याओं का प्रदर्शन कहा जाता है संख्यात्मक अनुक्रम.

    संख्यात्मक अनुक्रम की संख्या की अवधारणा में कई मूलभूत परिभाषाएं हैं:

    • $ ए $ की संख्या $ (x_n) $ (x_n) सीमा कहलाती है, यदि किसी भी $ \\ Varepsilon\u003e 0 $ के लिए $ \\ Varepsilon $ के आधार पर $ N N $ है, जैसे कि किसी भी नंबर के लिए $ n \u003e N $ असमानता $ \\ Left | x_n-a \\ राइट |
    • $ ए $ की वास्तविक संख्या को $ (x_n) $ (x_n) सीमा कहा जाता है, यदि $ (X_N) $ अनुक्रम के सभी सदस्य $ ए $ के किसी भी पड़ोस में हैं, तो शायद सदस्यों की एक सीमित संख्या को छोड़कर ।

    संख्यात्मक अनुक्रम की संख्या के मूल्य की गणना करने का एक उदाहरण मानें:

    उदाहरण 1।

    सीमा $ (\\ mathop (lim) _ (n \\ \\ unfty) \\ frac (n ^ 2-3n + 2) (2n ^ 2-n - 1) \\) $ खोजें

    फेसला:

    इस कार्य को हल करने के लिए, पहले, हमें ब्रैकेट के लिए अभिव्यक्ति में एक वरिष्ठ डिग्री बनाने की आवश्यकता है:

    $ (\\ Mathop (lim) _ (n \\ to \\ unfty) \\ frac (n ^ 2-3n + 2) (2n ^ 2 - n - 1) \\) \u003d (\\ mathop (lim) _ (x \\) Infty) \\ frac (n ^ 2 \\ बाएं (1- \\ frac (3) (n) + \\ frac (2) (n ^ 2) \\ दाएं)) (n ^ 2 \\ बाएं (2- \\ frac (1) (एन) - \\ frac (1) (n ^ 2) \\ दाएं)) \\) \u003d (\\ mathop (lim) _ (n \\ \\ unfty) \\ frac (1- \\ frac (3) (n) + \\ Frac (2) (n ^ 2)) (2- \\ frac (1) (n) - \\ frac (1) (n ^ 2)) \\) $

    यदि denominator एक असीम रूप से बड़ा मूल्य खर्च करता है, तो पूरी सीमा शून्य, $ \\ mathop (lim) _ (n \\ करने के लिए \\ unfty) \\ frac (1) (n) \u003d 0 $ के लिए प्रयास कर रही है, हम इसे प्राप्त करते हैं:

    $ (\\ Mathop (lim) _ (n \\ to \\ unfty) \\ frac (1- \\ frac (3) (n) + \\ frac (2) (n ^ 2)) (2- \\ frac (1) (n ) - \\ frac (1) (n ^ 2)) \\) \u003d \\ frac (1-0 + 0) (2-0-0) \u003d \\ frac (1) (2) $

    उत्तर: $ \\ Frac (1) (2) $।

    बिंदु पर अवधारणा सीमा समारोह

    बिंदु पर समारोह की सीमा की अवधारणा में दो शास्त्रीय परिभाषाएं हैं:

      कौची की "सीमा" शब्द की परिभाषा

      मान्य संख्या $ a $ $ x \\ bept (x \\ दाएँ) की सीमा $ x \\ के साथ $ x] की सीमा कहा जाता है, यदि किसी भी $ \\ varepsilon\u003e 0 $ $ \\ delta\u003e 0 $ $ \\ Varepsilon $ के आधार पर मौजूद है जैसे x ^ (\\ backslash a) में किसी भी $ x \\ के लिए $ $ \\ Left की असमानता को संतुष्ट करना | xa \\ अधिकार |

      हेन द्वारा परिभाषा

      वास्तविक संख्या $ a $ को $ x \\ bept (x \\ दाएँ) $ x के साथ $ x \\ _ के साथ $ की सीमा कहा जाता है, यदि किसी भी अनुक्रम के लिए $ $ (x_n) \\ x $ में $ a $ a $ f (x_n) $ के मानों का क्रम $ A $ तक अभिसरण करता है।

    ये दो परिभाषाएं जुड़ी हुई हैं।

    नोट 1।

    कौची और हेन पर समारोह की सीमा की परिभाषा समतुल्य हैं।

    समारोह की सीमाओं की गणना के लिए क्लासिक दृष्टिकोण के अलावा, सूत्र को याद करें जो इसमें भी मदद कर सकता है।

    समकक्ष कार्यों की तालिका जब $ x $ असीम रूप से छोटा है (शून्य पर जाता है)

    सीमा समाधान के लिए एक दृष्टिकोण है समकक्ष समारोह के प्रतिस्थापन का सिद्धांत। समकक्ष कार्यों की तालिका इसे उपयोग करने के लिए नीचे प्रस्तुत किया गया है, दाईं ओर के कार्यों की बजाय अभिव्यक्ति के लिए उपयुक्त प्राथमिक फ़ंक्शन को प्रतिस्थापित करना आवश्यक है।

    चित्रा 1. समारोह समकक्ष तालिका। लेखक 24 - छात्र इंटरनेट एक्सचेंज

    साथ ही, उन सीमाओं को हल करने के लिए जिनके मान अनिश्चितता में कम हो जाते हैं, लोपिक नियम को लागू करना संभव है। आम तौर पर, $ \\ FRAC (0) (0) (0) $ की अनिश्चितता को गुणक पर संख्या और denominator फैलाने के लिए और फिर कम करने के लिए प्रकट किया जा सकता है। फॉर्म $ \\ FRAC (\\ INFTY) (\\ INFTY) (\\ unfty) $ होने वाले अनिश्चितता को एक संख्या में अभिव्यक्तियों को विभाजित करने और चर के लिए एक वैल्यूएटर को विभाजित करने के बाद हल किया जा सकता है, जिस पर पुरानी डिग्री स्थित है।

    अद्भुत सीमाएं

    • पहली अद्भुत सीमा:

    $ (\\ Mathop (lim) _ (x \\ to 0) \\ frac (sinx) (x) \\) \u003d 1 $

    • दूसरी अद्भुत सीमा:

    $ \\ Mathop (lim) _ (x \\ to 0) ((1 + x)) ^ (\\ frac (1) (x)) \u003d e $

    विशेष सीमाएं

    • पहली विशेष सीमा:

    $ \\ Mathop (lim) _ (x \\ to 0) \\ frac (((लॉग) _a (1 + x -) \\)) (x) \u003d ((लॉग) _a e \\) \u003d \\ frac (1) (lna ) $

    • दूसरी विशेष सीमा:

    $ \\ Mathop (lim) _ (x \\ to 0) \\ frac (a ^ x-1) (x) \u003d lna $

    • तीसरी विशेष सीमा:

    $ \\ mathop (lim) _ (x \\ to 0) \\ frac (((1 + x)) ^ (\\ mu) -1) (x) \u003d \\ MU $

    निरंतरता समारोह

    परिभाषा 2।

    फंक्शन $ F (x) $ को पॉइंट $ x \u003d x_0 $ पर निरंतर कहा जाता है, यदि $ \\ Forall \\ Varepsilon\u003e (\\ rm 0) $ \\ _ delta (\\ Varepsilon, e_ (0))\u003e (\\ rm 0) $ $ \\ Left | f (x) -f (x_ (0)) \\ राइट |

    फंक्शन $ एफ (एक्स) $ पॉइंट $ x \u003d x_0 $ पर निरंतर है, यदि $ \\ mathop ((\\ rm lim \\;)) \\ limits _ ((\\ rm x) \\ (\\ rm x) _ ( \\ rm 0))) f (x) \u003d f (x_ (0)) $।

    $ X_0 \\ in x $ को पहली प्रकार को तोड़ने का बिंदु कहा जाता है यदि $ \\ mathop (lim) _ (x \\ x_0-0) F (x_0) \\) $ (x_0) \\) की अंतिम सीमाएं हैं \\ mathop (lim) _ (x \\ th_0 + 0) f (x_0) \\) $, लेकिन समानता $ (\\ mathop (lim) _ (x \\ x_0-0) f (x_0) \\) \u003d (\\) mathop (lim) _ (x \\ x_0 + 0) f (x_0) \\) \u003d f (x_0) $

    और यदि $ (\\ mathop (lim) _ (x \\ th_0-0) f (x_0) \\) \u003d (\\ mathop (lim) _ (x \\ x_0 + 0) f (x_0) \\) \\ n ( x_0) $, तो यह डिस्पोजेबल अंतर का बिंदु है, और यदि $ (\\ mathop (lim) _ (x \\ to x_0-0) f (x_0) \\) \\ n (\\ mathop (lim) _ (x \\) x_0 + 0) f (x_0) \\) $, फिर कूद समारोह का बिंदु।

    एक्स $ पॉइंट में $ x_0 \\ को दूसरी प्रकार को तोड़ने का एक बिंदु कहा जाता है यदि $ (\\ mathop (lim) _ (x \\ x_0-0) F (x_0) \\) $ की सीमा में से एक है , $ (\\ mathop (lim) _ (x \\ to x_0 + 0) f (x_0) \\) $ अनंत है या मौजूद नहीं है।

    उदाहरण 2।

    $ Y \u003d \\ frac (2) (x) $ की निरंतरता का अन्वेषण करें

    फेसला:

    $ (\\ Mathop (lim) _ (x \\ tho 0-0) f (x) \\) \u003d (\\ mathop (lim) _ (x \\ tho 0-0) \\ frac (2) (x) \\) \u003d - - \\ Infty $ - फ़ंक्शन में दूसरी प्रकार को तोड़ने का एक बिंदु है।

    इसी तरह के लेख