Таким макаром, основной принцип деления конечных и безграничных повторяющихся дробей состоит в подмене этих дробей обычными дробями и следующем делении обычных дробей. Поделить десятичную дробь на 0,1; 0,01; 0,001 и т.д. Выполним деление десятичной дроби на натуральное число столбиком.

Математика 6 класс. Деление дробей

10, 100, 1000 и т.д. Начнем с общих принципов деления десятичных дробей. Допишем пару нулей справа в записи дроби 65,14, при всем этом получим равную ей десятичную дробь 65,1400 (смотрите равные и неравные десятичные дроби). Мы пришли к остатку 0, на этом шаге деление столбиком завершается.

Перенесем на право на 3 знака запятую в делимом и делителе. Разумеется, в делителе не хватает цифр для переноса запятой, потому допишем нужное количество нулей справа. Отныне начинают повторяться остатки 4, 19, 1, 10, 16 и 13, а означает, будут повторяться и числа 1, 9, 0, 4, 7 и 6 в личном.

При всем этом следует быть очень внимательным с делением повторяющихся дробей, чтоб не ошибиться с периодом дроби , которая выходит в итоге деления. Например, 7,5(716):0,01=757,(167), потому что после переноса запятой в записи десятичной дроби 7,5716716716… на два знака на право, имеем запись 757,167167….

Часть 2 из 2: Деление в столбик.

Для этого запишите делимое (обычно это большее число) слева, а делитель (число, на которое делят) справа. Вы получите задачку на деление в столбик с целыми числами. Если вы не помните, как разделять в столбик, перейдите в последующий раздел. Найдите первую цифру личного (результата деления).

В нашем примере делимым является число 30. 2-ая цифра делимого – это 0. Спустите ее вниз, записав 0 около 3 (итог вычитания). Приобретенный итог разделите на делитель. Для этого разделите число, расположенное на самой нижней строке, на делитель. В нашем примере разглядим цифру 3. Помножьте ее на делитель: 12 х 3 = 36. Потому что 36 больше 30, то цифра 3 не подходит.

Повторите описанные выше шаги, чтоб отыскать последующую цифру. Описанный метод употребляется в хоть какой задачке на деление в столбик. В нашем примере: 30 — 24 = 6. Запишите приобретенный итог (6) на новейшей строке.

В случае необходимости воспользуйтесь десятичной запятой, чтоб расширить делимое. Если делимое делится на делитель нацело, то на последней строке вы получите цифру 0. Это значит, что задачка решена, а ответ (в виде целого числа) записан под делителем. Но если в самом низу столбика находится неважно какая цифра, хорошая от 0, нужно расширить делимое, поставив десятичную запятую и приписав 0. Напомним, что это не меняет значения делимого.

Вы получите число 60. Сейчас разделите это число на делитель: 60 ÷ 12 = 5. Напишите 5 после 2 (и после десятичной запятой) под делителем. Есть задачки, когда делить в столбик можно нескончаемо длительно. В данном случае остановитесь и округлите ответ. К примеру, 17 ÷ 4,20 = 4,047619…

Часть 1 из 2: Перепишите задачку в другой форме.

Многие школьники к старшим классам запамятывают, как делать деление в столбик. Делитель – число, на которое будут разделять. То, что в итоге получится, именуется личное. Для деления в строку употребляется знак, схожий на двоеточие — «: », а при делении в столбик употребляют значок «∟», его еще по-другому именуют уголок. Запись этих чисел и математические деяния с ними, вточности такие же, как и с целыми числами.

Каждый школьник должен знать как разделять десятичные дроби на десятичную дробь. Если и делимое, и делитель помножить на однообразное число, то ответ, т. е. личное не поменяется. К примеру, при умножении десятичной дроби на 10, запятая сместится на одно число на право. Чтоб поделить десятичную дробь на натуральное число в столбик, необходимо сделать подобающую запись уголком, поделить.

Если десятичную дробь помножить на 0,0, 1000 и т. д. , то запятая, после целого числа изменит свое положение – она перенесется на право на столько же цифр, сколько нулей в числе, на которое помножили.

Читайте также:

Не пропусти:

Хлорофиллипт для деток: описание и факты Когда и для чего применяется масляный раствор Хлорофиллипта, а когда – спиртовой? При […] Ценность Тобольск Компания ООО ЛДЦ "БЕРЕГИНЯ" находится по адресу 626150, ОБЛАСТЬ ТЮМЕНСКАЯ, ГОРОД […] Несколько аспектов по допплерометрии плода при беременности При перенашивании, резус-конфликте и сладком диабете мамы доплер УЗИ при беременности […]

Сентябрь 26, 2016 Комментариев нет Елена Хиди Учебный.

Навигация по записям.

Свежайшие записи.

Веб-сайт работает наWordPress. Тема Vito разработанаQuema Labs.

Тезисы

Как разделять дробь на целое число. Как делить дробь на целое число. Время от времени для вас необходимо поделить дробь на целое число. Как разделить дробь на целое число бабушкино. Как разделять смешанные дроби. Как разделять смешанные дроби. Смешанное число Помножьте целое число на знаменатель дробной. Как поделить дробь на целое число. Как поделить дробь на целое число. Как дроби на целое число . делить на целое число. Деление дробей. Чтобы разделить дробь на натуральное число , надо знаменатель дроби умножить на число, а. Как разделить целое число на дробь. чтобы делить целое число на число на порядок дроби и потом как дроби 3/5 и 0. Как делить дроби? Как разделить число на дробь | Математика. данное число умножить на число, обратное дроби целое число. на число Как делить. Как разделить смешанную дробь на натуральное число . Как разделить смешанную дробь на натуральное число а целое число дроби умножить на. Как делить дроби | Математика. Чтобы понять, как делить дроби, изучим правило и на примерах рассмотрим, как его применять.

В этой статье мы разберем деление целых чисел без остатка. Здесь мы будем говорить лишь о делении таких целых чисел, абсолютные величины которых делятся нацело (смотрите смысл деления натуральных чисел без остатка). Про деление целых чисел с остатком мы побеседуем в отдельной статье.

Сначала мы введем термины и обозначения, которые будем использовать для описания деления целых чисел. Дальше укажем смысл деления целых чисел, который поможет нам получить правила деления целых положительных, целых отрицательных и целых чисел с разными знаками. Здесь же мы рассмотрим примеры применения правил деления целых чисел. Наконец, мы покажем, как выполняется проверка результата деления целых чисел.

Навигация по странице.

Термины и обозначения

Целое число, которое делят, называется делимым . Целое число, на которое проводится деление, называется делителем . Результат деления целых чисел называется частным .

Деление обозначается символом вида:, который располагается между делимым и делителем (иногда встречается символ ÷, который также обозначает деление). Деление целого числа a на целое число b можно записать с использованием символа: как a:b . Если в результате деления целого числа a на целое число b получается число c , то этот факт удобно записывать в виде равенства a:b=c . вида a:b также называют частным, как и значение этого выражения.

Смысл деления целых чисел

Мы знаем о существовании связи между умножением и делением натуральных чисел . Из этой связи мы заключили, что деление – это нахождение неизвестного множителя, когда известен второй множитель и произведение. Делению целых чисел придадим этот же смысл. То есть, деление целых чисел – это нахождение по данному произведению и одному из целых множителей другого целого множителя.

Исходя из смысла деления целых чисел, мы можем сказать, что если произведение двух целых чисел a и b равно c , то частное от деления c на a равно b , и частное от деления c на b равно a . Приведем пример. Допустим нам известно, что произведение двух целых чисел 5 и −7 равно −35 , тогда мы можем сказать, что частное (−35):5 равно −7 , а частное (−35):(−7) равно 5 .

Отметим, что частное от деления целого числа a на целое число b является целым числом (если a делится на b без остатка).

Правила деления целых чисел

Смысл деления целых чисел, указанный в предыдущем пункте, позволяет утверждать, что один из двух множителей является частным от деления их произведения на другой множитель. Но он не дает способа нахождения неизвестного множителя по известному множителю и произведению. Например, равенство 6·(−7)=−42 позволяет нам сказать, что частные (−42):6 и (−42):(−7) равны соответственно −7 и 6 . Однако если нам известно, что произведение двух множителей равно 45 и один из множителей равен −5 , то смысл деления целых чисел нам не дает прямого ответа на вопрос, чему равен другой множитель.

Эти рассуждения приводят нас к следующему выводу: нам нужны правила, позволяющие выполнять деление одного целого числа на другое. Сейчас мы их и получим. Эти правила позволят нам свести деление целых чисел к делению натуральных чисел.

Деление целых положительных чисел

Целые положительные числа – это натуральные числа , поэтому деление целых положительных чисел проводится по всем правилам деления натуральных чисел . Здесь больше нечего добавить, стоит лишь рассмотреть решение пары примеров, в которых проводится деление целых положительных чисел.

Пример.

Выполните деление целого положительного числа 104 на целое положительное число 8 .

Решение.

Делимое 104 в данном случае можно представить в виде суммы 80+24 , после чего воспользоваться правилом деления суммы на данное число . Получаем 104:8=(80+24):8=80:8+24:8=10+3=13 .

Ответ:

104:8=13 .

Правило деления целых отрицательных чисел, примеры

Сформулировать правило деления целых отрицательных чисел нам помогут следующие рассуждения.

Пусть нам нужно разделить целое отрицательное число a на целое отрицательное число b . Обозначим буквой c искомое частное от деления a на b , то есть, a:b=c . Выясним сначала, чему равна c .

В силу смысла деления целых чисел должно быть справедливо равенство b·c=a . Тогда . позволяют нам записать равенство , следовательно, . Из полученного равенства следует, что , то есть, абсолютная величина частного от деления равна частному от деления модулей делимого и делителя .

Осталось определить знак числа c . Другими словами выясним, положительным или отрицательным целым числом является результат деления целых отрицательных чисел.

По смыслу деления целых чисел справедливо равенство b·c=a . Тогда из правил умножения целых чисел следует , что число c должно быть положительным. В противном случае b·c будет являться произведением целых отрицательных чисел, которое по правилу умножения будет равно произведению модулей множителей, следовательно, будет положительным числом, а у нас число a – целое отрицательное. Таким образом, частное c от деления целых отрицательных целых чисел есть целое положительное число .

Теперь объединим сделанные выводы в правило деления целых отрицательных чисел. Чтобы разделить целое отрицательное число на целое отрицательное число, нужно модуль делимого разделить на модуль делителя . То есть, если a и b – целые отрицательные числа, то .

Рассмотрим применение правила деления целых отрицательных чисел при решении примеров.

Пример.

Разделите целое отрицательное число −92 на целое отрицательное число −4 .

Решение.

По правилу деления целых отрицательных чисел искомый результат равен частному от деления модуля делимого на модуль делителя. Получаем .

Ответ:

(−92):(−4)=23 .

Пример.

Вычислите частное (−512):(−32) .

Решение.

Нам нужно выполнить деление целых отрицательных чисел, воспользуемся соответствующим правилом. Модуль делимого равен 512 , модуль делителя равен 32 . Осталось разделить 512 на 32 . Выполним деление столбиком:

Ответ:

(−512):(−32)=16 .

Правило деления целых чисел с разными знаками, примеры

Получим правило деления целых чисел с разными знаками.

Пусть мы делим целое число a на целое число b (знаки чисел a и b различны, то есть, если a – целое положительное число, то b – отрицательное, а если a – отрицательное, то b – положительное число) и в результате получаем число c .

В предыдущем пункте этой статьи мы выяснили, что модуль частного равен частному от деления модуля делимого на модуль делителя, то есть, . Теперь мы можем вычислить абсолютную величину частного от деления целых чисел с разными знаками. Осталось выяснить знак числа c .

Смысл деления целых чисел нам дает равенство b·c=a . Возможны два варианта: либо a – положительное целое число, b – отрицательное; либо a – отрицательное целое число, b – положительное. В любом из этих случаев, в силу правил умножения целых чисел, число c должно быть отрицательным. Действительно, по правилам умножения целых чисел, если и b и c отрицательные целые числа, то их произведение будет положительным числом, а если b положительное, c – отрицательное, то их произведение есть отрицательное число.

Теперь мы можем сформулировать правило деления целых чисел с разными знаками. Чтобы разделить целые числа с разными знаками, нужно разделить модуль делимого на модуль делителя, и перед полученным числом поставить знак минус . То есть, если a и b – целые числа с разными знаками, то .

Разберем решения примеров, в которых применяется правило деления целых чисел с разными знаками.

Пример.

Разделите целое положительное число 56 на целое отрицательное число −4 .

Решение.

Будем действовать согласно правилу деления целых чисел с разными знаками. Модуль делимого равен 56 , модуль делителя равен 4 . Вычислим частное от деления модуля делимого на модуль делителя: 56:4=14 . Перед полученным числом осталось поставить знак минус, имеем −14 .

Таким образом, при делении целых чисел с разными знаками 56 и −4 мы получили число −14 .

Ответ:

56:(−4)=−14 .

Пример.

Выполните деление целого числа −1 625 на 25 .

Решение.

Нам нужно провести деление целых чисел с разными знаками. Воспользуемся полученным правилом деления: (1 625 можно разделить на 25 в столбик, или представить 1 625 в виде суммы 1 500+125 и воспользоваться правилом деления суммы на данное число).

Ответ:

(−1 625):25=−65 .

Деление нуля на целое число

Отдельно нужно остановиться на делении нуля на целое число, отличное от нуля. В этих случаях правило деления таково: частное от деления нуля на любое целое число, отличное от нуля, равно нулю . То есть, 0:b=0 для любого целого и отличного от нуля числа b .

Приведем пояснения озвученного правила деления нуля на целое число. Предположим, что в результате деления нуля на целое число b (b не равно нулю) получается число c . Тогда по смыслу деления целых чисел должно быть справедливо равенство b·c=0 . Мы знаем, что произведение двух целых чисел равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю (об этом мы упоминали в разделе теории умножение целого числа на нуль). Так как b не равно нулю, значит, нулю должен быть равен множитель c . Следовательно, частное от деления нуля на целое число, отличное от нуля, равно нулю.

Приведем несколько примеров. Частное от деления 0 на целое отрицательное число −908 равно 0 , частное 0:4 также равно нулю.

На нуль делить нельзя

Деление целого числа на нуль не определяется. Другими словами, на нуль делить нельзя.

Почему же так? Давайте предположим, что при делении целого числа a на нуль получается целое число c . Тогда по смыслу деления целых чисел справедливо равенство c·0=a . Из правила умножения целого числа на нуль следует, что c·0=0 , каким бы не было число c . Сопоставляя два полученных равенства, делаем вывод, что если делимое a отлично от нуля, то равенство c·0=a будет неверным, что свидетельствует о том, что на нуль нельзя делить число, отличное от нуля.

А можно ли делить нуль на нуль? Давайте предположим, что при делении нуля на нуль получается целое число c , тогда в силу смысла деления целых чисел должно быть верно равенство c·0=0 . Это равенство действительно верно, но оно верно не только для какого-то конкретного целого числа c , но и вообще для любого числа c . Иными словами, результатом деления нуля на нуль можно принять любое целое число. Так вот чтобы избежать этой многозначности, решили не рассматривать деление на нуль.

Итак, делить на нуль нельзя.

Проверка результата деления целых чисел

Проверка результата деления целых чисел осуществляется при помощи умножения. Чтобы проверить, правильно ли было проведено деление целых чисел, нужно полученное частное умножить на делитель, если в результате получится число, равное делимому, то результат деления правильный .

Рассмотрим решение примера, в котором выполняется проверка результата деления целых чисел.

Говорят: «Математика – гимнастика ума». Воистину, верные слова. Вычисления, производимые в уме, без калькулятора, карандаша и других «подручных инструментов», прекрасно развивают мозг. Кроме того, вы приобретаете уверенность в том, что в случае непредвиденных обстоятельств, спокойно обойдетесь собственными силами.

Еще несколько десятков лет назад в школах был такой предмет – «Устный счет», на занятиях школьники учились вычислять в уме – умножать, делить, складывать и вычитать числа. Из собственного опыта все мы знаем, что делить в уме намного сложнее, чем, например, умножать. Для того чтобы делить устно, нужно знать методику сокращенного деления и, естественно, таблицу умножения. Например, есть способ, который поможет вашему ребенку научиться быстро делить на 5.

Как это делается?

Метод быстрого деления на 5 очень прост. Естественно, он подразумевает, что ребенок таблицу умножения помнит «на зубок». Для примера мы не будем брать числа, которые в таблице умножения есть, и ваш ученик их хорошо помнит. Возьмем что-то более сложное. Например:

Как мы помним, умножать легче, чем делить. А умножать на 2 – под силу практически всем школьникам. Так вот, чтобы быстро разделить любое число на 5, его нужно сначала умножить на 2! То, что получится в результате умножения, является почти ответом на вопрос: «Сколько будет, если разделить число на 5?» Только нужно в числе произведения последнюю цифру отделить запятой.

Проверим?

Берем число 165, умножаем его на 2, в результате получаем 330. Отделяем в этом числе последнюю цифру, то есть ноль, и получаем число 33. Именно это число и является результатом деления числа 165 на 5. Вот так просто, можете проверить на калькуляторе.

Продолжаем.

• 238х2 = 476.

• 482х2 = 964.

• 1026х2 = 2052.

Просто, как все гениальное.

И еще одно. Если уже мы говорим об устном счете, то для таких вычислений нужно тренировать память: это необходимо, чтобы удерживать в голове все расчеты.

Кстати, если у вашего школьника хорошо развита зрительная память, он может попробовать мысленно делить «в столбик». Этот метод не такой «скоростной», как предыдущий, но как вариант может использоваться.

Улучшить навыки счета поможет IQКлуб

Развить навыки счета, улучшить память, внимание, мышление, расширить кругозор вашего ребенка поможет интернет-сервис IQКлуб. Команда профессионалов, в которую вошли ученые, программисты, дизайнеры, педагоги, психологи, разработали специальные, очень увлекательные игры для детей. С учетом их возраста рассчитана нагрузка в обучающих программах.

Разработчики игр позаботились о том, чтобы они не содержали рекламы и платного контента. Интерактивное обучение, без сомнения, заинтересует современного ребенка. Его досуг будет интересным и, главное, полезным. А родители смогут контролировать процесс обучения в режиме онлайн.

Как же воспользоваться услугами сервиса IQКлуб?

1. Зарегистрируйтесь в системе.
2. Ваш ребенок проходит несложный, но занимательный тест.
3. Специальный алгоритм оценивает способности вашего малыша.
4. Для вашего ребенка формируется индивидуальная программа обучения.

Все! Заниматься можно в любом месте, где есть доступ к сети Интернет. Развивающие игры на сайте предназначены для детей от 3 до 14 лет. 13 тысяч родителей уже сотрудничают с новым интернет-сервисом IQКлуб, который имеет в своем арсенале более 90 полезных игр.

В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0 , 1 , 0 , 01 , 100 , 10 и др.

Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.

Yandex.RTB R-A-339285-1

Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.

Пример 1

Разделите 1 , 2 на 0 , 48 .

Решение

Запишем десятичные дроби в виде обыкновенных. У нас получится:

1 , 2 = 12 10 = 6 5

0 , 48 = 48 100 = 12 25 .

Таким образом, нам надо разделить 6 5 на 12 25 . Считаем:

1 , 2: 0 , 48 = 6 2: 12 25 = 6 5 · 25 12 = 6 · 25 5 · 12 = 5 2

Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 2 1 2 , а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 5 2 = 2 , 5 . О том, как это сделать, мы уже писали ранее.

Ответ: 1 , 2: 0 , 48 = 2 , 5 .

Пример 2

Посчитайте, сколько будет 0 , (504) 0 , 56 .

Решение

Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.

0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111

После этого конечную десятичную дробь также переведем в другой вид: 0 , 56 = 56 100 . Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:

0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 · 100 56 = 100 111

У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:

Ответ: 0 , (504) : 0 , 56 = 0 , (900) .

Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.

Пример 3

Найдите, сколько будет 0 , 779 … / 1 , 5602 .

Решение

Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:

0 , 779 … ≈ 0 , 78

1 , 5602 ≈ 1 , 56

Можем продолжить подсчеты и получить примерный результат: 0 , 779 … : 1 , 5602 ≈ 0 , 78: 1 , 56 = 78 100: 156 100 = 78 100 · 100 156 = 78 156 = 1 2 = 0 , 5 .

Точность результата будет зависеть от степени округления.

Ответ: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .

Как разделить натуральное число на десятичную дробь и наоборот

Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.

Пример 4

Разделите 2 , 5 на 45 .

Решение

Приведем 2 , 5 к виду обыкновенной дроби: 255 10 = 51 2 . Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:

25 , 5: 45 = 51 2: 45 = 51 2 · 1 45 = 17 30

Если перевести результат в десятичную запись, то мы получим 0 , 5 (6) .

Ответ: 25 , 5: 45 = 0 , 5 (6) .

Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.

Определение 1

Для деления столбиком десятичных дробей на натуральные числа необходимо:

1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).

2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.

Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.

Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.

Пример 5

Вычислите, сколько будет 65 , 14 4 .

Решение

Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65 , 1400 , которая будет равна исходной. Теперь пишем столбик для деления на 4:

Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:

Мы добрались до нулевого остатка, следовательно, процесс деления завершен.

Ответ: 65 , 14: 4 = 16 , 285 .

Пример 6

Разделите 164 , 5 на 27 .

Решение

Делим сначала дробную часть и получаем:

Отделяем полученную цифру запятой и продолжаем делить:

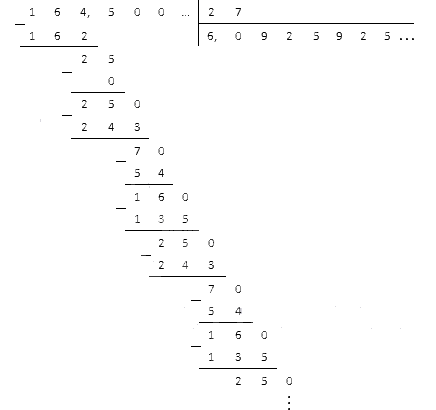
Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6 , 0 (925) .

Ответ: 164 , 5: 27 = 6 , 0 (925) .

Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на 10 , 100 и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:

a: b = (a · 10) : (b · 10) , a: b = (a · 100) : (b · 100) и так далее.

Сформулируем правило:

Определение 2

Для деления одной конечной десятичной дроби на другую необходимо:

1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.

2. После этого делим дробь столбиком на получившееся натуральное число.

Разберем конкретную задачу.

Пример 7

Разделите 7 , 287 на 2 , 1 .

Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби 72 , 87 на 21 . Запишем полученные числа столбиком и вычислим

Ответ: 7 , 287: 2 , 1 = 3 , 47

Пример 8

Вычислите 16 , 3 0 , 021 .

Решение

Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:

Видим периодическое повторение остатков 4 , 19 , 1 , 10 , 16 , 13 . В частном повторяются 1 , 9 , 0 , 4 , 7 и 5 . Тогда наш результат является периодической десятичной дробью 776 , (190476) .

Ответ: 16 , 3: 0 , 021 = 776 , (190476) ​​​​​​

Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.

Пример 9

Подсчитайте, сколько будет 3 5 , 4 .

Решение

Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению 30 , 0 на 54 . Запишем данные столбиком и вычислим результат:

Повторение остатка дает нам в итоге число 0 , (5) , которое является периодической десятичной дробью.

Ответ: 3: 5 , 4 = 0 , (5) .

Как разделить десятичные дроби на 1000, 100, 10 и др.

Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1 / 1000 , 1 / 100 , 1 / 10 и др. Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.

Пример 10

Так, 56 , 21: 10 = 5 , 621 , а 0 , 32: 100 000 = 0 , 0000032 .

В случае с бесконечными десятичными дробями мы поступаем таким же образом.

Пример 11

Например, 3 , (56) : 1 000 = 0 , 003 (56) и 593 , 374 … : 100 = 5 , 93374 … .

Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.

Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на 1000 , 100 , 10 соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.

Пример 12

К примеру, 5 , 739: 0 , 1 = 57 , 39 и 0 , 21: 0 , 00001 = 21 000 .

Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.

Так, 7 , 5 (716) : 0 , 01 = 757 , (167) , поскольку после того, как мы перенесли запятую в записи десятичной дроби 7 , 5716716716 … на два знака вправо, у нас получилось 757 , 167167 … .

Если же у нас в примере непериодические дроби, то все обстоит проще: 394 , 38283 … : 0 , 001 = 394382 , 83 … .

Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот

Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.

Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Найдите первую цифру частного (результата деления). Для этого разделите первую цифру делимого на делитель. Результат напишите под делителем.

• В нашем примере первой цифрой делимого является цифра 3. Разделите 3 на 12. Так 3 меньше 12, то результатом деления будет 0. Запишите 0 под делителем – это первая цифра частного.

Умножьте полученный результат на делитель. Напишите результат умножения под первой цифрой делимого, так как эту цифру вы только что разделили на делитель.

• В нашем примере 0 × 12 = 0, поэтому напишите 0 под 3.

Вычтите результат умножения из первой цифры делимого. Запишите ответ на новой строке.

• В нашем примере: 3 - 0 = 3. Напишите 3 непосредственно под 0.

Спустите вниз вторую цифру делимого. Для этого запишите следующую цифру делимого рядом с результатом вычитания.

• В нашем примере делимым является число 30. Вторая цифра делимого – это 0. Спустите ее вниз, записав 0 возле 3 (результат вычитания). Вы получите число 30.

Полученный результат разделите на делитель. Вы найдете вторую цифру частного. Для этого разделите число, расположенное на самой нижней строке, на делитель.

• В нашем примере разделите 30 на 12. 30 ÷ 12 = 2 плюс некоторый остаток (так как 12 х 2 = 24). Напишите 2 после 0 под делителем – это вторая цифра частного.
• Если вы не можете найти подходящую цифру, перебирайте цифры до тех пор, пока результат умножения какой-либо цифры на делитель не окажется меньше и ближе всего к числу, расположенное последним в столбике. В нашем примере рассмотрим цифру 3. Умножьте ее на делитель: 12 х 3 = 36. Так как 36 больше 30, то цифра 3 не подходит. Теперь рассмотрим цифру 2. 12 х 2 = 24. 24 меньше 30, поэтому цифра 2 является верным решением.

Повторите описанные выше шаги, чтобы найти следующую цифру. Описанный алгоритм используется в любой задаче на деление в столбик.

• Умножьте вторую цифру частного на делитель: 2 х 12 = 24.
• Напишите результат умножения (24) под последним числом в столбике (30).
• Вычтите меньшее число из большего. В нашем примере: 30 - 24 = 6. Запишите полученный результат (6) на новой строке.

Если в делимом остались цифры, которые можно спустить вниз, продолжите процесс вычисления. В противном случае перейдите к следующему шагу.

• В нашем примере вы спустили вниз последнюю цифру делимого (0). Поэтому переходите к следующему шагу.

В случае необходимости воспользуйтесь десятичной запятой, чтобы расширить делимое. Если делимое делится на делитель нацело, то на последней строке вы получите цифру 0. Это означает, что задача решена, а ответ (в виде целого числа) записан под делителем. Но если в самом низу столбика находится любая цифра, отличная от 0, необходимо расширить делимое, поставив десятичную запятую и приписав 0. Напомним, что это не меняет значения делимого.

• В нашем примере на последней строке находится цифра 6. Поэтому справа от 30 (делимое) напишите десятичную запятую, а затем напишите 0. Также десятичную запятую поставьте после найденных цифр частного, которые вы записываете под делителем (после этой запятой пока ничего не пишите!).

Повторите описанные действия, чтобы найти следующую цифру. Главное не забудьте поставить десятичную запятую как после делимого, так и после найденных цифр частного. В остальном процесс аналогичен процессу, описанному выше.

• В нашем примере спустите вниз 0 (который вы написали после десятичной запятой). Вы получите число 60. Теперь разделите это число на делитель: 60 ÷ 12 = 5. Напишите 5 после 2 (и после десятичной запятой) под делителем. Это третья цифра частного. Таким образом, окончательный ответ: 2,5 (нулем перед 2 можно пренебречь).