Среди функциональных рядов наиболее важное место занимают степенные ряды.

Степенным рядом называют ряд

члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x , а c 0 , c 1 , c 2 , c n - постоянные величины. Числа c 1 , c 2 , c n - коэффициенты членов ряда, c 0 - свободный член. Члены степенного ряда определены на всей числовой прямой.

Ознакомимся с понятием области сходимости степенного ряда. Это множество значений переменной x , для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox .

При подстановке в степенной ряд значения x = 0 получится числовой ряд

c 0 +0+0+...+0+... ,

который сходится.

Следовательно, при x = 0 сходится любой степенной ряд и, значит, область его сходимости не может быть пустым множеством. Структура области сходимости всех степенных рядов одинакова. Её можно установить с помощью следующей теоремы.

Теорема 1 (теорема Абеля) . Если степенной ряд сходится при некотором значении x = x 0 , отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x | < |x 0 | . Обратите внимание: и отправное значение "икс нулевое" и любое значение "икса", которое сравнивается с отправным, взяты по модулю - без учёта знака.

Следствие. Если степенной ряд расходится при некотором значении x = x 1 , то он расходится и при всех значениях |x | > |x 1 | .

Как мы уже выяснили ранее, любой степенной ряд сходится при значении x = 0. Есть степенные ряды, которые сходятся только при x = 0 и расходятся при остальных значениях х . Исключая из рассмотрения этот случай, предположим, что степенной ряд сходится при некотором значении x = x 0 , отличном от нуля. Тогда, по теореме Абеля, он сходится во всех точках интервала ]-|x 0 |, |x 0 |[ (интервала, левой и правой границами которого являются значения икса, при котором степенной ряд сходится, взятые соответственно со знаком минус и со знаком плюс), симметричного относительно начала координат.

Если же степенной ряд расходится при некотором значении x = x 1 , то на основании следствия из теоремы Абеля он расходится и во всех точках вне отрезка [-|x 1 |, |x 1 |] . Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый интервалом сходимости , в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться, при чем не обязательно одновременно, а вне отрезка ряд расходится. Число R называется радиусом сходимости степенного ряда.

В частных случаях интервал сходимости степенного ряда может вырождаться в точку (тогда ряд сходится только при x = 0 и считается, что R = 0) или представлять собой всю числовую прямую (тогда ряд сходится во всех точках числовой прямой и считается, что ).

Таким образом, определение области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследовании сходимости ряда на границах интервала сходимости (при ).

Теорема 2. Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при отношения абсолютных величин коэффициентов общего следующего за ним членов ряда, т.е..

Пример 1. Найти область сходимости степенного ряда

Решение. Здесь

Используя формулу (28), найдём радиус сходимости данного ряда:

Исследуем сходимость ряда на концах интервала сходимости . В примере 13 показано, что данный ряд сходится при x = 1 и расходится при x = -1. Следовательно, областью сходимости служит полуинтервал .

Пример 2. Найти область сходимости степенного ряда

Решение. Коэффициенты ряда положительны, причём

Найдём предел этого отношения, т.е. радиус сходимости степенного ряда:

Исследуем сходимость ряда на концах интервала . Подстановка значений x = -1/5 и x = 1/5 в данный ряд даёт:

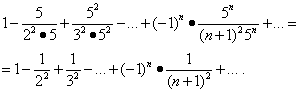
Первый из этих рядов сходится (см. пример 5). Но тогда в силу теоремы параграфа «Абсолютная сходимость» сходится и второй ряд, а область его сходимости – отрезок

Пример 3. Найти область сходимости степенного ряда

Решение. Здесь

По формуле (28) находим радиус сходимости ряда:

Исследуем сходимость ряда при значениях . Подставив их в данный ряд, соответственно получим

Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при ). Итак, на обоих концах интервала сходимости данный ряд расходится, а область его сходимости – интервал .

Пример 5. Найти область сходимости степенного ряда

Решение. Находимо отношение , где , а :

Согласно формуле (28) радиус сходимости данного ряда

,

то есть ряд сходится только при x = 0 и расходится при остальных значениях х .

Примеры показывают, что на концах интервала сходимости ряды ведут себя различно. В примере 1 на одном конце интервала сходимости ряд сходится, а на другом – расходится, в примере 2 – на обоих концах сходится, в примере 3 – на обоих концах расходится.

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать с помощью признака Даламбера , или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.

Пример 6. Найти интервал сходимости степенного ряда

Решение. Данный ряд не содержит членов с нечётными степенями х . Поэтому преобразуем ряд, полагая . Тогда получим ряд

для нахождения радиуса сходимости которого можно применить формулу (28). Так как , а , то радиус сходимости этого ряда

Из равенства получаем , следовательно, данный ряд сходится на интервале .

Сумма степенного ряда. Дифференцирование и интегрирование степенных рядов

Пусть для степенного ряда

радиус сходимости R > 0, т.е. этот ряд сходится на интервале .

Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f (x ) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f (x ) на интервале сходимости.

Вне интервала сходимости равенство (30) не имеет смысла.

Пример 7. Найти сумму сумму степенного ряда

Решение. Это геометрический ряд, у которого a = 1, а q = x . Следовательно, его сумма есть функция . Ряд сходится, если , а - его интервал сходимости. Поэтому равенство

справедливо лишь для значений , хотя функция определена для всех значений х , кроме х = 1.

Можно доказать, что сумма степенного ряда f (x ) непрерывна и дифференцируема на любом отрезке внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.

Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.

Теорема 1. Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны .

Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х , если , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны

Разложение функций в степенные ряды

Пусть дана функция f (x ), которую требуется разложить в степенной ряд, т.е. представить в виде (30):

Задача состоит в определении коэффициентов ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:

……………………………………………….. (31)

Полагая в равенствах (30) и (31) х = 0, находим

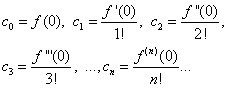
Подставляя найденные выражения в равенство (30), получим

(32)

Найдём разложение в ряд Маклорена некоторых элементарных функций.

Пример 8. Разложить в ряд Маклорена функцию

Решение. Производные этой функции совпадают с самой функцией:

Поэтому при х = 0 имеем

Подставляя эти значения в формулу (32), получим искомое разложение:

(33)

Этот ряд сходится на всей числовой прямой (его радиус сходимости ).

Если функция f(x) имеет на некотором интервале, содержащем точку а , производные всех порядков, то к ней может быть применена формула Тейлора:

где r n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:

, где число x заключено между х и а .

Если для некоторого значения х r n ®0 при n ®¥, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора :

Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х , если:

1) она имеет производные всех порядков;

2) построенный ряд сходится в этой точке.

При а =0 получаем ряд, называемый рядом Маклорена :

Пример 1 f(x)= 2 x .

Решение . Найдем значения функции и ее производных при х =0

f(x) = 2 x , f(0) = 2 0 =1;

f¢(x) = 2 x ln2, f¢(0) = 2 0 ln2= ln2;

f¢¢(x) = 2 x ln 2 2, f¢¢(0) = 2 0 ln 2 2= ln 2 2;

f (n) (x) = 2 x ln n 2, f (n) (0) = 2 0 ln n 2= ln n 2.

Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -¥