Tarp funkcinių serijų svarbiausią vietą užima galios serijos.

Galios serija yra serija

kurių nariai yra galios funkcijos, išdėstyti didėjančiais sveikųjų skaičių neneigiamomis galiomis x, A c 0 , c 1 , c 2 , c n – pastovios reikšmės. Skaičiai c 1 , c 2 , c n – eilės terminų koeficientai, c 0 – laisvas narys. Laipsnių eilučių sąlygos apibrėžtos visoje skaičių eilutėje.

Susipažinkime su koncepcija laipsnių eilučių konvergencijos sritis. Tai kintamųjų reikšmių rinkinys x, kurio serija sutampa. Galios eilutės turi gana paprastą konvergencijos sritį. Už tikrosios vertybės kintamasis x konvergencijos sritis susideda arba iš vieno taško, arba yra tam tikras intervalas (konvergencijos intervalas), arba sutampa su visa ašimi Jautis .

Keičiant į galios serija vertybes x= 0 bus skaičių serija

c 0 +0+0+...+0+... ,

kuris susilieja.

Todėl kai x= 0 bet kuri laipsnio eilutė suartėja ir todėl jos konvergencijos sritis negali būti tuščias rinkinys. Visų laipsnių eilučių konvergencijos srities struktūra yra vienoda. Jį galima nustatyti naudojant šią teoremą.

1 teorema (Abelio teorema). Jei laipsnio eilutė suartėja ties kokia nors verte x = x 0, skiriasi nuo nulio, tada jis suartėja ir, be to, absoliučiai visoms | x| < |x 0 |

. Atkreipkite dėmesį: ir pradinė reikšmė „X yra nulis“, ir bet kuri „X“ reikšmė, kuri lyginama su pradine reikšme, imama modulo – neatsižvelgiant į ženklą. Pasekmė. Jeigu galios serijos skiriasi x = x tam tikra verte x| > |x 1 | .

1, tada jis skiriasi visoms | reikšmėms x Kaip jau sužinojome anksčiau, bet kuri laipsnio eilutė suartėja su verte x= 0. Yra laipsnių eilučių, kurios susilieja tik tada, kai = 0 ir kitoms reikšmėms skiriasi X x = x. Neatsižvelgdami į šį atvejį, darome prielaidą, kad laipsnio eilutė suartėja ties tam tikra verte x 0 |, |x 0, skiriasi nuo nulio. Tada, pagal Abelio teoremą, jis suartėja visuose intervalo ]-| taškuose

0 |[ (intervalas, kurio kairioji ir dešinioji ribos yra x reikšmės, kuriose laipsnių eilutė suartėja, atitinkamai paimta su minuso ir pliuso ženklu), simetriškas kilmei. x = x Jei galios eilutė skiriasi tam tikra verte x 1 |, |x 1 |] . Iš to išplaukia, kad bet kuriai laipsnio eilei yra intervalas, simetriškas pradžios atžvilgiu, vadinamas konvergencijos intervalas, kiekviename taške, kurio eilutė suartėja, ties ribomis ji gali suartėti arba gali skirtis, ir nebūtinai tuo pačiu metu, o už atkarpos ribų serija skiriasi. Skaičius R vadinamas laipsnių eilučių konvergencijos spinduliu.

Ypatingais atvejais laipsnių eilučių konvergencijos intervalas gali išsigimti iki taško (tada serija susilieja tik tada, kai x= 0 ir laikoma, kad R= 0) arba vaizduoti visą skaičių tiesę (tada serija suartėja visuose skaičių linijos taškuose ir daroma prielaida, kad ).

Taigi, laipsnio eilutės konvergencijos srities nustatymas susideda iš jos nustatymo konvergencijos spindulys R ir tiriant eilučių konvergenciją ties konvergencijos intervalo ribomis (prie ).

2 teorema. Jei visi laipsnio eilutės koeficientai, pradedant nuo tam tikro, skiriasi nuo nulio, tada jos konvergencijos spindulys yra lygus ribai, kuri yra bendrųjų narių koeficientų absoliučių verčių santykiu. ją sekančios serijos, t.y.

1 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Čia

Naudodami (28) formulę randame šios eilutės konvergencijos spindulį:

Ištirkime eilučių konvergenciją konvergencijos intervalo galuose. Tai rodo 13 pavyzdys ši serija susilieja ties x= 1 ir skiriasi ties x= -1. Vadinasi, konvergencijos sritis yra pusės intervalas.

2 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Serijos koeficientai yra teigiami, ir

Raskime šio santykio ribą, t.y. laipsnių eilučių konvergencijos spindulys:

Išnagrinėkime eilučių konvergenciją intervalo galuose. Vertės pakeitimas x= -1/5 ir x= 1/5 šioje eilutėje suteikia:

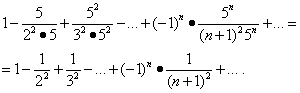
Pirmoji iš šių eilučių suartėja (žr. 5 pavyzdį). Bet tada, remiantis „absoliučios konvergencijos“ skyriaus teorema, antroji eilutė taip pat suartėja, o jos konvergencijos sritis yra segmentas

3 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Čia

Naudodami (28) formulę randame eilučių konvergencijos spindulį:

Išnagrinėkime reikšmių eilučių konvergenciją. Pakeitę juos šioje serijoje, gauname atitinkamai

Abi eilutės skiriasi, nes neįvykdyta būtina sąlyga konvergencija (jų bendrieji terminai nėra linkę į nulį ties ). Taigi abiejuose konvergencijos intervalo galuose ši eilutė skiriasi, o jos konvergencijos sritis yra intervalas.

5 pavyzdys. Raskite laipsnių eilučių konvergencijos sritį

Sprendimas. Mes randame santykį, kur , ir :

Pagal (28) formulę šios eilutės konvergencijos spindulys

,

tai yra, serija susilieja tik tada, kai x= 0 ir skiriasi kitoms reikšmėms = 0 ir kitoms reikšmėms skiriasi.

Pavyzdžiai rodo, kad konvergencijos intervalo pabaigoje eilutės elgiasi skirtingai. 1 pavyzdyje viename konvergencijos intervalo gale konverguoja, o kitame, 2 pavyzdyje, ji suartėja abiejuose galuose;

Laipsnių eilutės konvergencijos spindulio formulė gaunama darant prielaidą, kad visi eilutės narių koeficientai, pradedant nuo tam tikro taško, skiriasi nuo nulio. Todėl (28) formulę galima naudoti tik šiais atvejais. Jei ši sąlyga pažeidžiama, laipsnių eilučių konvergencijos spindulio reikia ieškoti naudojant d'Alembert testą arba, pakeičiant kintamąjį, seką transformuoti į formą, kurioje tenkinama nurodyta sąlyga.

6 pavyzdys. Raskite laipsnių eilučių konvergencijos intervalą

Sprendimas. Šioje serijoje nėra terminų su nelyginiais laipsniais = 0 ir kitoms reikšmėms skiriasi. Todėl transformuojame seriją, nustatymą . Tada gauname seriją

rasti kurio konvergencijos spindulį galime pritaikyti (28) formulę. Kadangi , a , tada šios serijos konvergencijos spindulys

Iš lygybės gauname Todėl ši serija suartėja su intervalu .

Galios eilučių suma. Galios eilučių diferencijavimas ir integravimas

Leiskite galios serijai

konvergencijos spindulys R> 0, t.y. ši serija susilieja į intervalą .

Tada kiekviena vertė = 0 ir kitoms reikšmėms skiriasi iš konvergencijos intervalo atitinka tam tikrą eilutės sumą. Todėl laipsnių eilučių suma yra funkcija = 0 ir kitoms reikšmėms skiriasi konvergencijos intervale. Žymėdamas tai f(x), galime parašyti lygybę

suprasti tai ta prasme, kad serijų suma kiekviename taške = 0 ir kitoms reikšmėms skiriasi iš konvergencijos intervalo yra lygus funkcijos reikšmei f(x) šiuo metu. Ta pačia prasme sakysime, kad laipsnio eilutė (29) konverguoja į funkciją f(x) konvergencijos intervale.

Už konvergencijos intervalo ribų lygybė (30) neturi prasmės.

7 pavyzdys. Raskite laipsnių eilučių sumą

Sprendimas. Tai geometrinė serija, kuriai a= 1, a q= x. Todėl jo suma yra funkcija . Serija konverguoja, jei , ir yra jos konvergencijos intervalas. Todėl lygybė

galioja tik reikšmėms, nors funkcija apibrėžtos visoms vertėms = 0 ir kitoms reikšmėms skiriasi, išskyrus = 0 ir kitoms reikšmėms skiriasi= 1.

Galima įrodyti, kad laipsnių eilutės suma f(x) yra tęstinis ir diferencijuojamas bet kuriame konvergencijos intervalo intervale, ypač bet kuriame eilutės konvergencijos intervalo taške.

Pateiksime teoremas apie laipsnių eilučių diferencijavimą ir integravimą.

1 teorema. Laipsninės eilutės (30) jos konvergencijos intervale gali būti diferencijuojamos pagal terminą neribotą skaičių kartų, o gautos laipsnių eilutės konvergencijos spindulys yra toks pat kaip ir pradinės eilutės, o jų sumos atitinkamai lygios .

2 teorema. Laipsnių eilutę (30) galima integruoti po terminą neribotą skaičių kartų intervale nuo 0 iki = 0 ir kitoms reikšmėms skiriasi, jei , ir gautos laipsnio eilutės turi tokį patį konvergencijos spindulį kaip ir pradinės eilutės, o jų sumos yra atitinkamai lygios

Funkcijų išplėtimas į galių eilutes

Tegu funkcija duota f(x), kurią reikia išplėsti į galios eilutę, t.y. pavaizduoti formoje (30):

Užduotis – nustatyti koeficientus eilutė (30). Norėdami tai padaryti, diferencijuodami lygybę (30) pagal terminą, nuosekliai randame:

……………………………………………….. (31)

Darant prielaidą, kad lygybės (30) ir (31) = 0 ir kitoms reikšmėms skiriasi= 0, randame

Rastus posakius pakeitę lygybe (30), gauname

(32)

Raskime kai kurių elementarių funkcijų Maclaurin serijos išplėtimą.

8 pavyzdys. Išplėskite funkciją Maclaurin serijoje

Sprendimas. Šios funkcijos išvestiniai sutampa su pačia funkcija:

Todėl kai = 0 ir kitoms reikšmėms skiriasi= 0 turime

Pakeitę šias reikšmes į (32) formulę, gauname norimą išplėtimą:

(33)

Ši eilutė susilieja į visą skaičių tiesę (jos konvergencijos spindulį).

Jei funkcija f(x) turi tam tikrame intervale, kuriame yra taškas A, visų eilių išvestiniai, tada jai galima pritaikyti Teiloro formulę:

Kur r n– vadinamasis liekanos narys arba eilutės liekana, ją galima įvertinti naudojant Lagranžo formulę:

, kur skaičius x yra tarp = 0 ir kitoms reikšmėms skiriasi Ir A.

Jei už kokią nors vertę x r n®0 val n®¥, tada riboje Teiloro formulė virsta konvergentine šios reikšmės formule Taylor serija:

Taigi funkcija f(x) galima išplėsti į Taylor seriją aptariamame taške = 0 ir kitoms reikšmėms skiriasi, Jei:

1) turi visų eilučių išvestines priemones;

2) sudarytos eilutės konverguoja šioje vietoje.

At A=0 gauname seriją, vadinamą netoli Maclaurino:

1 pavyzdys f(x)= 2x.

Sprendimas. Raskime funkcijos ir jos išvestinių reikšmes = 0 ir kitoms reikšmėms skiriasi=0

f(x) = 2x, f( 0) = 2 0 =1;

f¢(x) = 2x ln2, f¢( 0) = 2 0 ln2= ln2;

f¢¢(x) = 2x 2 2, f¢¢( 0) = 2 0 ln 2 2 = ln 2 2;

f(n)(x) = 2x ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.

Pakeisdami gautas išvestinių vertes į Taylor serijos formulę, gauname:

Šios eilutės konvergencijos spindulys yra lygus begalybei, todėl šis išplėtimas galioja -¥