Netinkami pirmosios rūšies integralai. Iš esmės tai yra tas pats apibrėžtasis integralas, tačiau tais atvejais, kai integralai turi begalinę viršutinę arba apatinę integravimo ribas arba abi integracijos ribos yra begalinės.

Netinkami antrojo tipo integralai. Iš esmės tai yra tas pats apibrėžtasis integralas, tačiau tais atvejais, kai integralas imamas iš neapribotų funkcijų, integrandas, esantis baigtiniame taškų skaičiuje, neturi baigtinio integravimo segmento, besisukančio į begalybę.

Palyginimui.Įvedant apibrėžtojo integralo sąvoką buvo daroma prielaida, kad funkcija f(x) yra tęstinis intervale [ a, b], o integravimo segmentas yra baigtinis, tai yra, jį riboja skaičiai, o ne begalybė. Dėl kai kurių užduočių reikia atsisakyti šių apribojimų. Taip atsiranda netinkami integralai.

Netinkamo integralo geometrinė reikšmė Pasirodo gana paprastai. Tuo atveju, kai funkcijos grafikas y = f(x) yra virš ašies Jautis, apibrėžtasis integralas išreiškia kreivinės trapecijos, apribotos kreive, plotą y = f(x) , x ašis ir ordinatės x = a , x = b. Savo ruožtu netinkamas integralas išreiškia neribotos (begalinės) kreivinės trapecijos, esančios tarp eilučių, plotą y = f(x) (paveikslėlyje žemiau - raudona), x = a ir abscisių ašį.

Netinkami integralai apibrėžiami panašiai ir kitiems begaliniams intervalams:

Begalinės kreivės trapecijos plotas gali būti baigtinis skaičius, tokiu atveju netinkamas integralas vadinamas konvergentiniu. Plotas taip pat gali būti begalinis, ir šiuo atveju netinkamas integralas vadinamas divergentiniu.

Integralo ribos naudojimas vietoj paties netinkamo integralo. Norint įvertinti netinkamą integralą, reikia naudoti apibrėžtojo integralo ribą. Jeigu ši riba egzistuoja ir yra baigtinė (nelygu begalybei), tai netinkamas integralas vadinamas konvergentiniu, o kitaip – ​​divergentiniu. Tai, kas kintamasis yra po ribinio ženklo, priklauso nuo to, ar mes susiduriame su netinkamu pirmosios ar antrosios rūšies integralu. Išsiaiškinkime apie tai dabar.

Netinkami pirmosios rūšies integralai – su begalinėmis ribomis ir jų konvergencija

Netinkami integralai su begaline viršutine riba

Taigi netinkamo integralo rašymas skiriasi nuo įprasto apibrėžtojo integralo tuo, kad viršutinė integralo riba yra begalinė.

Apibrėžimas. Netinkamas integralas su begaline viršutine tolydžios funkcijos integravimo riba f(x) intervale nuo a į ∞ vadinama šios funkcijos integralo riba su viršutine integravimo riba b ir apatinė integracijos riba a su sąlyga, kad viršutinė integracijos riba auga neribotai, t.y.

.

Jei ši riba egzistuoja ir yra lygi tam tikram skaičiui, o ne begalybei, tada netinkamas integralas vadinamas konvergentiniu, o jo reikšme laikomas skaičius, kuriam lygi riba. Priešingu atveju netinkamas integralas vadinamas divergentiniu ir jam nepriskiriama jokia prasmė.

1 pavyzdys. Apskaičiuokite netinkamą integralą(jei jis susilieja).

Sprendimas. Remdamiesi netinkamo integralo apibrėžimu, randame

Kadangi riba egzistuoja ir lygi 1, tai tai netinkamas integralas konverguoja ir yra lygus 1.

Šiame pavyzdyje integrandas yra beveik toks pat kaip 1 pavyzdyje, tik laipsnis x yra ne du, o raidė alfa, o užduotis yra ištirti netinkamą integralą konvergencijai. Tai reiškia, kad dar reikia atsakyti į klausimą: ties kokiomis alfa reikšmėmis šis netinkamas integralas susilieja, o prie kokių – skiriasi?

2 pavyzdys. Ištirkite konvergencijos netinkamą integralą(apatinė integracijos riba yra didesnė už nulį).

Sprendimas. Pirmiausia manykime, kad tada

Gautoje išraiškoje pereiname prie ribos:

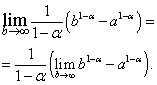
Nesunku pastebėti, kad riba dešinėje egzistuoja ir yra lygi nuliui kai , tai yra, ir neegzistuoja, kai , tai yra .

Pirmuoju atveju, tai yra, kai . Jei, tada ir neegzistuoja.

Mūsų tyrimo išvada yra tokia: tai netinkamas integralas konverguoja ir skiriasi adresu .

Niutono-Leibnizo formulės taikymas tiriamo netinkamo integralo tipui , galite gauti šią formulę, kuri yra labai panaši į ją:

.

Tai apibendrinta Niutono-Leibnizo formulė.

3 pavyzdys. Apskaičiuokite netinkamą integralą(jei jis susilieja).

Egzistuoja šio integralo riba:

Antrasis integralas, sudarantis pradinį integralą išreiškiančią sumą:

Taip pat egzistuoja šio integralo riba:

.

Randame dviejų integralų sumą, kuri yra ir pradinio netinkamo integralo su dviem begalinėmis ribomis vertė:

Netinkami antrojo tipo integralai – iš neribotų funkcijų ir jų konvergencijos

Tegul funkcija f(x) pateikta segmente nuo a į b ir yra neribotas. Tarkime, kad funkcija taške eina į begalybę b , o visuose kituose atkarpos taškuose jis yra tęstinis.

Apibrėžimas. Netinkamas funkcijos integralas f(x) segmente nuo a į b vadinama šios funkcijos integralo riba su viršutine integravimo riba c , jei kai stengiamasi c Į b funkcija didėja neribotai, ir taške x = b funkcija neapibrėžta, t.y.

.

Jei ši riba egzistuoja, tai antros rūšies netinkamas integralas vadinamas konvergentiniu, kitu atveju jis vadinamas divergentiniu.

Naudodami Niutono-Leibnizo formulę išvedame.

Netinkamas integralas su begaline integravimo riba

Kartais toks netinkamas integralas dar vadinamas netinkamu pirmosios rūšies integralu..gif" width="49" height="19 src=">.

Mažiau paplitę integralai su begaline apatine riba arba su dviem begalinėmis ribomis: .

Mes apsvarstysime populiariausią atvejį https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Ne, ne visada. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Brėžinyje pavaizduokime integrando funkcijos grafiką. Tipiškas grafikas ir lenkta trapecija šiuo atveju atrodo taip:

Netinkamas integralashttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", kitaip tariant, sritis taip pat yra begalinė. Gali buti taip.Šiuo atveju jie sako, kad netinkamas integralas skiriasi.

2) Bet. Kad ir kaip paradoksaliai tai skambėtų, begalinės figūros plotas gali būti lygus... baigtiniam skaičiui! Pavyzdžiui: .. Antruoju atveju netinkamasis integralas susilieja.

Kas atsitiks, jei begalinė lenkta trapecija yra žemiau ašies?.gif" width="217" height="51 src=">.

: .

1 pavyzdys

Integralo funkcija https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, o tai reiškia, kad viskas gerai ir netinkamą integralą galima apskaičiuoti naudojant „ standartinis“ metodas.

Mūsų formulės taikymas https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

Tai yra, netinkamas integralas skiriasi, o užtamsintos kreivės trapecijos plotas yra lygus begalybei.

Sprendžiant netinkamus integralus labai svarbu žinoti, kaip atrodo pagrindinių elementariųjų funkcijų grafikai!

2 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

Padarykime piešinį:

Pirma, atkreipiame dėmesį į tai: integrandas yra tęstinis pusės intervale. Geras..gif" width="327" height="53">

(1) Imame paprasčiausią galios funkcijos integralą (šis specialus atvejis yra daugelyje lentelių). Geriau nedelsiant įdėti minusą už ribos ženklo, kad jis netrukdytų tolesniems skaičiavimams.

(2) Viršutinę ir apatinę ribas pakeičiame naudodami Niutono-Leibnizo formulę.

(3) Atkreipiame dėmesį, kad https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Ponai, tai reikia suprasti ilgai prieš laiką) ir supaprastinkite atsakymą.

Čia begalinės lenktos trapecijos plotas yra baigtinis skaičius! Neįtikėtina, bet tiesa.

3 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

Integrandas yra nuolatinis.

Pirmiausia pabandykime surasti antiderivatinę funkciją (neapibrėžtą integralą).

Į kurį iš lentelės integralų panašus integrandas? Tai man primena arctangentą: . Šie svarstymai rodo, kad būtų puiku, jei vardiklyje būtų kvadratas. Tai atliekama pakeičiant.

Pakeiskime:

Visada naudinga atlikti patikrinimą, tai yra diferencijuoti gautą rezultatą:

Dabar randame netinkamą integralą:

(1) Rašome sprendimą pagal formulę . Geriau iš karto perkelti konstantą už ribos ženklo, kad ji netrukdytų tolesniems skaičiavimams.

(2) Viršutinę ir apatinę ribas pakeičiame pagal Niutono-Leibnizo formulę..gif" width="56" height="19 src=">? Arktangento grafiką žr. jau ne kartą rekomenduojamame straipsnyje.

(3) Gauname galutinį atsakymą. Faktas, kurį naudinga žinoti mintinai.

Pažengę studentai gali neieškoti neapibrėžtinio integralo atskirai ir nenaudoti pakeitimo metodo, o naudoti funkciją pakeisti po diferencialiniu ženklu ir netinkamą integralą išspręsti „nedelsiant“. Šiuo atveju sprendimas turėtų atrodyti maždaug taip:

“

Integravimo funkcija yra nuolatinė adresu https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“

4 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

! Tai tipiškas pavyzdys, o panašūs integralai randami labai dažnai. Padirbk gerai! Antiderivatinė funkcija čia randama naudojant viso kvadrato išskyrimo metodą.

5 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

Šis integralas gali būti išspręstas detaliai, tai yra, pirmiausia reikia rasti neapibrėžtą integralą, pakeitus kintamąjį. Arba galite tai išspręsti „nedelsiant“ - funkciją įtraukdami po diferencialo ženklu.

Netinkami neapribotų funkcijų integralai

Kartais tokie netinkami integralai vadinami antrosios rūšies netinkamais integralais. Netinkami antrojo tipo integralai yra klastingai „užšifruoti“ įprastu apibrėžtuoju integralu ir atrodo lygiai taip pat: ..gif" width="39" height="15 src=">, 2) arba taške , 3) arba abiejuose taškuose iš karto, 4) arba net apie integravimo segmentą. Straipsnio pabaigoje yra nuoroda į papildomą pamoką.

Tik pavyzdys, kad būtų aišku: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, tada mūsų vardiklis pateks į nulį, tai yra, integrandas šiuo metu tiesiog neegzistuoja!

Apskritai, analizuojant netinkamą integralą visada turite pakeisti abi integravimo ribas į integrandą..jpg" alt="Netinkamas integralas, nutrūkimo taškas ties apatine integravimo riba" width="323" height="380">!}

Čia viskas beveik taip pat, kaip ir pirmosios rūšies integrale.
Mūsų integralas yra skaitiniu požiūriu lygus tamsintos kreivės trapecijos plotui, kuris nėra ribojamas iš viršaus. Šiuo atveju gali būti dvi galimybės: netinkamas integralas skiriasi (plotas yra begalinis) arba netinkamas integralas yra lygus baigtiniam skaičiui (ty begalinės figūros plotas yra baigtinis!).

Belieka modifikuoti Niutono-Leibnizo formulę. Ji taip pat yra modifikuojama ribos pagalba, bet riba jau linksta ne į begalybę, o vertintihttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> teisingai.

6 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

Integrandas turi begalinį nenutrūkstamumą taške (nepamirškite žodžiu arba juodraštyje patikrinti, ar viskas gerai su viršutine riba!)

Pirmiausia apskaičiuokime neapibrėžtą integralą:

Pakeitimas:

Apskaičiuokime netinkamą integralą:

(1) Kas čia naujo? Kalbant apie sprendimų technologiją, praktiškai nieko nėra. Vienintelis dalykas, kuris pasikeitė, yra įrašas po limito piktograma: . Papildymas reiškia, kad mes siekiame reikšmės dešinėje (tai yra logiška – žr. grafiką). Tokia riba ribų teorijoje vadinama vienpuse riba. Šiuo atveju turime dešiniarankių ribą.

(2) Viršutinę ir apatinę ribas pakeičiame naudodami Niutono-Leibnizo formulę.

(3) Supraskime https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Kaip nustatyti, kur turėtų būti posakis? Grubiai tariant , tereikia pakeisti reikšmę, pakeisti tris ketvirčius ir nurodyti, kad šukos atsakymas.

Šiuo atveju netinkamas integralas yra lygus neigiamam skaičiui.

7 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

8 pavyzdys

Apskaičiuokite netinkamą integralą arba nustatykite jo divergenciją.

Jei integrandas taške neegzistuoja

Begalinė lenkta tokio netinkamo integralo trapecija iš esmės atrodo taip:

Čia viskas yra visiškai tas pats, išskyrus tai, kad mūsų riba yra linkusi vertintihttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> turime priartėti be galo arti lūžio taško paliko.

2Netinkami pirmosios rūšies integralai vadinami formos integralais. Laikoma, kad integrandas yra tęstinis visoje integracijos atkarpoje.

2 Jei riba egzistuoja ir yra baigtinė, tada sakoma, kad netinkamas integralas suartėja ir yra lygus

Integralai ir apibrėžiami panašiai:

(8.21)
Kur A– bet koks tikrasis skaičius. Be to, apie paskutinį integralą jie sako, kad jis konverguoja tada ir tik tada, kai susilieja abu jį sudarantys integralai.

8.10 uždavinys.

Sprendimas.

Todėl integralas išsiskiria.

8.11 uždavinys. Apskaičiuokite netinkamą integralą.

Sprendimas.

Šis integralas susilieja.

2 Netinkami antrojo tipo integralai vadinami integralais formos: , kur integrandas yra f(x) turi begalinius netolydumus baigtiniame atkarpoje [ a; b]. Netinkami antrosios rūšies integralai apibrėžiami skirtingai, atsižvelgiant į pertrūkių taškų vietą intervale [ a; b].

1) Tarkime, kad funkcija f(x) turi begalinį pertrūkį tam tikrame vidiniame integracijos srities taške ( cÎ( a; b)) Kituose atkarpos taškuose [ a; b] funkcija laikoma tęstine.

Tada, jei ribos ir egzistuoja ir yra baigtinės, tada jie sako, kad integralas suartėja ir yra lygus

. (8.22)
2) Tegul vienintelis funkcijos nutrūkimo taškas f(x) sutampa su tašku A

. (8.23)
3) Tegul vienintelis funkcijos nutrūkimo taškas f(x) sutampa su tašku b. Tada, jei riba egzistuoja ir yra baigtinė, tada jie sako, kad integralas suartėja ir yra lygus

. (8.24)
Daroma prielaida, kad e > 0 ir d > 0.

8.12 uždavinys. Apskaičiuokite netinkamą integralą.

Sprendimas. x= 2. Todėl

8.13 uždavinys. Apskaičiuokite netinkamą integralą.

Sprendimas. Integrandas taške turi antrojo tipo nenutrūkstamumą x= 0 (integracijos regione). Vadinasi,

Pirmoji riba egzistuoja ir yra baigtinė, tačiau antroji riba yra lygi begalybei (at). Todėl šis integralas skiriasi.

9 skyrius. Kelių kintamųjų funkcijos

§9.1. Apibrėžimas n-dimensinė Euklido erdvė Rn.

Prieš pereinant prie daugelio kintamųjų funkcijų tyrimo, naudinga pristatyti sąvoką n-dimensinė erdvė bet kokiam n = 1, 2, 3,… .

2 taškas x n-dimensinė erdvė (vektorius) yra sutvarkyta kolekcija n realūs skaičiai.

Skambina numeriu i vektoriaus koordinatė.

2 Atstumas tarp dviejų taškų n-dimensinė erdvė ir nustatoma pagal formulę:

Atstumas nuo taško iki taško x vadinamas vektoriaus moduliu x ir yra paskirtas. Iš (9.1) formulės išplaukia, kad .

IN n-dimensinė erdvė, natūraliai įvedama skaliarinio sandaugos sąvoka:

Kampas tarp vektorių x Ir y galima nustatyti pagal formulę:

Kaip ir anksčiau, vektoriai x Ir y yra statmenos tada ir tik tada, kai jų skaliarinė sandauga yra lygi nuliui.

2Visų taškų rinkinys n-dimensinė erdvė, kurioje atstumas apibrėžiamas pagal (9.1) formulę, o skaliarinė sandauga vadinama n-dimensinė Euklido vektorinė erdvė ir žymima .

Tuo atveju n= 1 tarpas sutampa su linija, tuo atveju n= 2 – su plokštuma, o byloje n= 3 – su tarpu.

2 Leiskite ir . Visų taškų rinkinys toks, kad , vadinamas n-išmatuotas rutulys su centru taške x arba e- taško kaimynystė x erdvėje ir žymimas .

Koordinačių forma šis apibrėžimas atrodo taip:

Esant tiesioginei linijai, t.y. adresu n= 1, taško kaimynystė yra intervalas, kurio centras yra spindulio taške e. Lėktuvo atveju, t.y. adresu n= 2, taško kaimynystė yra atviras apskritimas, kurio centras yra spindulio taške e. Kosmoso atveju, t.y. adresu n= 3 taško kaimynystė yra atviras rutulys, kurio centras yra spindulio taške e.

§9.2. Kelių kintamųjų funkcijos apibrėžimo sritis. Tęstinumas

2 Funkcija n kintamieji yra taisyklė (dėsnis), pagal kurią kiekviena aibė, susidedanti iš n kintamieji, paimti iš tam tikros srities Dn-dimensinė erdvė, priskiriama vienam skaičiui z. Paprasčiausiu atveju.

2 2 kintamųjų funkcija yra taisyklė (dėsnis), pagal kurią kiekvienas taškas M(x; y), priklausantis kokiai nors sričiai D lėktuvas xOy, atitinka vienaskaitos skaičių z.

Daugelis erdvės taškų su koordinatėmis sudaro tam tikrą paviršių (9.1 pav.), kylantį virš ploto D(geometrinė dviejų kintamųjų funkcijos reikšmė).

2 Plotas D, kuriai sukonstruotas aukščiau pateiktas atitikimas, vadinamas funkcijos apibrėžimo sritimi.

9.1 problema. Raskite funkcijos sritį

Sprendimas. Reikalinga apibrėžimo sritis yra taškų rinkinys plokštumoje xOy, tenkinantis nelygybių sistemą. Nelygybės ir pakeisti jų ženklą į priešingą (atitinkamai), kai susikerta šios tiesės: x = y Ir x = 0, y= 0. Šios tiesės dalija plokštumą xOy 6 regionams. Nuosekliai, pakeitę savavališkus taškus iš kiekvienos srities į sistemą, esame įsitikinę, kad domenų (1) ir (3) sąjunga yra pradinės funkcijos apibrėžimo sritis. Be to, jis yra tiesus x = y, išskyrus tašką (0; 0), yra įtrauktas į apibrėžimo sritį ir tiesias linijas x= 0 ir y= 0 – neįtraukta (9.2 pav.).

2 Regiono uždarymas yra erdvės taškų rinkinys, kurio bet kurioje kaimynystėje yra regiono taškai D.

Tegu pvz. D– tam tikra atvira (riba neįtraukta) lėktuve xOy. Tada regionas bus uždarytas, jei į regioną D pritvirtinkite jo kraštą G .

2 Leiskite tam tikroje srityje D lėktuvas xOy funkcija yra suteikta, ir tegul yra tam tikras regiono uždarymo taškas D(). Skaičius A vadinama funkcijos riba taške M 0, jei bet koks skaičius e> 0 yra toks skaičius δ > 0, kuri visiems taškams, išskyrus tašką M 0 ir mažesniu nei vienu atstumu nuo jo δ , nelygybė tenkinama.

2 Funkcija taške vadinama tęstine, jei ji apibrėžta šiame taške () ir galioja lygybė.

§9.3. Dviejų kintamųjų funkcijos lygio linijos

2 linijos plokštumoje xOy, pateiktos lygtimis , kur SU– savavališka konstanta, vadinama funkcijos lygio linijomis.

Lygio linijos – tai paviršiaus, tam tikros funkcijos ir plokštumos susikirtimo linijos z = C, lygiagrečiai plokštumai xOy. Naudodami lygio linijas galite ištirti funkcijos nurodytą paviršiaus formą.

9.2 pavyzdys. Raskite lygio linijas ir nustatykite lygties pateiktą paviršiaus formą.

Lygių linijų lygtys šiuo atveju turi formą . Pas C< 0 уравнение дает пустое множество решений (следовательно, вся поверхность расположена выше плоскости xOy). At C= 0 tik vienas taškas tenkina lygio linijos lygtį x = 0, y= 0 (su plokštuma xOy paviršius susikerta tik koordinačių pradžioje). At C> 0 lygio linijos yra elipsės, su pusiau ašimis ir . Lygio linijos, atitinkančios skirtingas reikšmes SU, parodyta pav. 9.3. Lygtimi apibrėžtas paviršius vadinamas elipsiniu paraboloidu (9.4 pav.).

§9.4. Pirmosios eilės dalinės išvestinės

Įsileiskite į kokią nors sritį D lėktuvas xOy funkcija yra duota ir yra tam tikras taškas regione D.

x

, (9.2)

2 Dalinė funkcijos išvestinė taške kintamojo atžvilgiu y(žymimas arba ) vadinamas

, (9.3)
jei ši riba egzistuoja ir yra baigtinė.

2 Dalinė išvestinė funkcija n kintamieji taške po kintamojo x i paskambino

, (9.4)
jei ši riba egzistuoja ir yra baigtinė.

Kaip matyti iš (9.2) – (9.4) formulių, dalinės išvestinės nustatomos taip pat, kaip buvo nustatyta vieno kintamojo funkcijos išvestinė. Skaičiuojant ribą, tik vienas iš kintamųjų prieaugio negauna ir išlieka pastovus. Vadinasi, dalinės išvestinės gali būti apskaičiuojamos taikant tas pačias taisykles kaip ir įprastos išvestinės, visus laisvuosius kintamuosius (išskyrus tą, pagal kurį diferencijuojama) traktuojant kaip konstantas.

9.3 problema. Raskite funkcijos dalines išvestines

Sprendimas. .

9.4 problema. Raskite funkcijos dalines išvestines.

Sprendimas. Skiriant duotąją funkciją kintamojo atžvilgiu x mes naudojame taisyklę laipsninei funkcijai diferencijuoti ir kai randame dalinę išvestinę kintamojo atžvilgiu y– eksponentinės funkcijos diferencijavimo taisyklė:

9.5 uždavinys. Apskaičiuokite funkcijos dalines išvestines taške.

Sprendimas. Taikydami kompleksinės funkcijos diferenciacijos taisyklę, randame dalines išvestines

Taško koordinačių pakeitimas dalinėmis išvestinėmis M, gauname

§9.5. Kelių kintamųjų funkcijos gradientas.
Kryptinė išvestinė

2 Funkcijos gradientas taške yra vektorius, sudarytas iš tam tikros funkcijos dalinių išvestinių, apskaičiuotų tam tikrame taške:

2 Funkcijos išvestinė taške vektoriaus kryptimi yra šios funkcijos gradiento vektoriaus projekcija, apskaičiuota taške M 0, šia kryptimi

Apskaičiavę vektoriaus projekciją į vektorių pagal (2.6) formulę, gauname

. (9.7)
Pastebėjus, kad kur a– kampas, kurį vektorius sudaro su ašimi JAUTIS, gauname dar vieną formulę išvestinei vektoriaus krypties atžvilgiu apskaičiuoti

9.6 problema. Raskite funkcijos gradientą taške M 0 (4; 2) ir išvestinė vektoriaus krypties atžvilgiu

Sprendimas. Raskime dalines išvestines

Apskaičiuokime dalinių išvestinių reikšmes taške M 0:

Funkcijos gradientas taške M 0 bus rasta naudojant (9.5) formulę:

9.7 problema. Taške M 0 (0; 1) apskaičiuokite funkcijos išvestinę antrojo koordinačių kampo bisektoriaus kryptimi.

Sprendimas. Raskime funkcijos dalines išvestines:

Apskaičiuokime dalinių išvestinių vertes ir funkcijos gradientą taške M 0:

Funkcijos taške išvestinė M 0 antrojo koordinačių kampo bisektoriaus kryptimi (ši kryptis yra su ašimi JAUTIS kampe a= 135°) galima rasti naudojant (9.8) formulę:

§9.6. Kelių kintamųjų funkcijos diferencialas
ir jo taikymas apytiksliems skaičiavimams

1 Jei taške funkcija turi nuolatines dalines išvestines ir , tada jos bendras prieaugis judant iš taško M 0 iki taško gali būti pavaizduotas taip:

, (9.9)
kur , .

2 Išraiška vadinama visuminiu funkcijos skirtumu taške.

Iš (9.9) formulės išplaukia, kad funkcijos diferencialas yra pagrindinė tiesinė visos funkcijos prieaugio dalis. Pakankamai mažam D x ir D y išraiška yra žymiai mažesnė už diferencialą ir gali būti nepaisoma. Taigi gauname tokią apytikslę formulę:

. (9.10)
komentuoti. Formulė (9.10) gali būti naudojama apytiksliai funkcijų reikšmėms apskaičiuoti tik pakankamai arti taško esančiuose taškuose. Kuo mažesnė reikšmė, tuo tikslesnė reikšmė rasta naudojant (9.9) formulę.

9.8 pavyzdys. Apskaičiuokite apytiksliai naudodami diferencialą.

Panagrinėkime funkciją. Reikia apskaičiuoti vertę z 1 šios funkcijos taške ( x 1 ; y 1) = (0,09; 6,95). Naudokime apytikslę formulę (9.9), tašku pasirinkdami tašką (0; 7). Tada D x = x 1 – x 0 = 0,09 – 0 = 0,09, D y =y 1 – y 0 = 6,95 – 7 = – 0,05.

Vadinasi,

§9.7. Aukštesnės eilės dalinės išvestinės priemonės

Įsileisti į teritoriją D pateikta funkcija, turinti ištisines dalines išvestines ir šioje srityje. Taigi, rajone D gavome dvi naujas nuolatines dviejų kintamųjų funkcijas ir . Jei tam tikru tašku srityje D funkcijos ir turi dalines išvestines tiek kintamojo atžvilgiu x, ir keičiant y, tada šios išvestinės vadinamos funkcijos antros eilės išvestinėmis. Jie žymimi taip:

1 Jei tam tikru srities tašku D funkcija turi ištisinių mišrių išvestinių ir , tada taške šios išvestinės yra lygios: .

D, turi būti įvykdytos šios sąlygos: D = 32 – 9 = 23. M Kadangi diskriminantas yra didesnis už nulį, tada taške A Ir SU funkcija turi ekstremumą. Būtent vietinis minimumas, nes

daugiau nei nulis. Tuo pačiu metu Skambino Netinkamas integralasIš funkcijos(FX) su begaline viršutine riba. Jei ši riba egzistuoja ir yra baigtinė, tada iškviečiamas netinkamas integralas Konvergentinis
. Bet jei jo nėra arba yra lygi ± ¥, tada šis netinkamas integralas vadinamas

Skirtingas. Iš funkcijos(F) ≥ 0 Jeigu F ≥ visiems A , Tai U

(6.2)

(6.3)

netinkamas integralas (6.1) turi akivaizdžią geometrinę reikšmę, kuri išplaukia iš įprasto apibrėžtojo integralo geometrinės reikšmės (4.3). Iš tiesų, pagal pav. 5.14 Čia¥ S - plotas, be galo išplėstas ašies kryptimi Oi kreivinė trapecija (5.15 pav.). Nepaisant begalinio masto, jis taip pat gali pasirodyti baigtinis. Bet taip gali nutikti, kaip rodo pav. 5.15, tik tuo atveju, kai = Iš funkcijos(F) → Y F → ¥ 0 val kreivinė trapecija (5.15 pav.). Nepaisant begalinio masto, jis taip pat gali pasirodyti baigtinis. Bet taip gali nutikti, kaip rodo pav. 5.15, tik tuo atveju, kai = Iš funkcijos(F) → Y F → ¥ . Ir net tada, jei funkcija

pakankamai greitai. 1 pavyzdys. Čia¥ Rasti sritį

,
, parodyta pav. 5.16. nuo ln → ¥ B nuo ln → ¥ .

adresu Čia¥ Taigi, F → ¥ = ¥. Ir tai nepaisant to, kad funkcija kada

. Netinkamas integralas, o tai reiškia, kad jis skiriasi. 2 pavyzdys. Čia¥ Rasti sritį

netinkamas integralas (6.1) turi akivaizdžią geometrinę reikšmę, kuri išplaukia iš įprasto apibrėžtojo integralo geometrinės reikšmės (4.3). Iš tiesų, pagal pav. 5.14 Čia¥ , parodyta pav. 5.17. F → ¥ = 1. Tai yra, be galo išplėsta sritis pasirodė esanti baigtinė. Taip atsitiko todėl, kad funkcija integrand at

3 pavyzdys . pakankamai greitai (bent jau daug greičiau nei integrandas ankstesniame pavyzdyje). Netinkamas integralas (skaičius), o tai reiškia, kad jis susilieja.

Išsiaiškinkite, ar netinkamas integralas suartėja, ar skiriasi. . Sprendimas

Apskaičiuokime šį integralą: kreivinė trapecija (5.15 pav.). Nepaisant begalinio masto, jis taip pat gali pasirodyti baigtinis. Bet taip gali nutikti, kaip rodo pav. 5.15, tik tuo atveju, kai= = Neegzistuoja. Tai akivaizdu, jei prisiminsime funkcijos grafiko elgesį F Nuodėmė F → ¥ (sinusoidai) ties F nelinkęs į nulį X →¥ .

Atkreipkite dėmesį, kad skaičiuodami netinkamus tipo integralus, taip pat skaičiuodami įprastus apibrėžtuosius integralus, galite iš karto pritaikyti Niutono-Leibnizo formulę:

Čia

Tikrai:

Jei vertė Iš funkcijos(¥ ) egzistuoja ir yra baigtinis, tai pagal Niutono-Leibnizo formulę (6.4) konverguoja ir netinkamasis integralas.

Pastaba. Visai analogiškai integralams su begaline viršutine riba, galima laikyti netinkamus integralus su begaline apatine riba ir net su abiem begalinėmis integravimo ribomis. Tai yra, formos integralai

Norėdami juos apskaičiuoti, taip pat galite naudoti Niutono-Leibnizo formulę.

4 pavyzdys.

adresu (skaičius), tai yra, šis integralas suartėja. Jo reikšmė π lygi plotui Čia¥ be galo išplėsta figūra abiem kryptimis, parodyta fig. 5.18.

Atkreipkite dėmesį, kad pats netinkamų integralų su begalinėmis integravimo ribomis konvergencijos-divergencijos faktas neturi būti nustatytas tiesiogiai apskaičiuojant šiuos integralus. Šį klausimą dažnai galima išspręsti daug paprasčiau, palyginus šį netinkamą integralą su kitu integralu, kuriam konvergencija-divergencija jau buvo nustatyta.

Tarkime, kad visiems yra nelygybė Iš funkcijos(F) £ G(F), Kur kreivinė trapecija (5.15 pav.). Nepaisant begalinio masto, jis taip pat gali pasirodyti baigtinis. Bet taip gali nutikti, kaip rodo pav. 5.15, tik tuo atveju, kai = Iš funkcijos(F) IR kreivinė trapecija (5.15 pav.). Nepaisant begalinio masto, jis taip pat gali pasirodyti baigtinis. Bet taip gali nutikti, kaip rodo pav. 5.15, tik tuo atveju, kai = G(F) - Dvi ištisinės ir neneigiamos funkcijos (5.19 pav.). Tada aišku, kad

Iš nelygybės (6.6) ir pav. 5.19 akivaizdžiai vadovaujasi vadinamuoju Netinkamų integralų palyginimo testas:

1) Jei (skaičius) suartėja, tada (skaičius) – susilieja, ir B 2) Jei - tada skiriasi - skiriasi. 3) Jei - skiriasi, tada - nieko negalima pasakyti apie šį integralą. 4) Jei (skaičius) - suartėja, tada - nieko negalima pasakyti apie šį integralą.

Kaip funkcija G(F) , su kuriuo ši funkcija lyginama intervale Iš funkcijos(F), funkcija dažnai naudojama, o integralas naudojamas kaip palyginimo integralas, atsižvelgiant į tai, kad kada visiems > 0 ir bet kuri α funkcija yra teigiama ir nuolatinė funkcija, ir tai

5 pavyzdys.

Sprendimas. Tai akivaizdu Jeigu F Î }